100. Чи можна забезпечити міцність похилих перерізів при згині за рахунок однієї поперечної арматури?
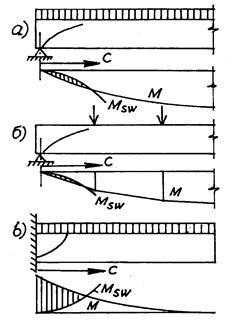
Відповісти на це питання найлегше, поєднавши на одній координатної осі епюру моментів M від зовнішнього навантаження з епюр несучої здатності поперечної арматури Msw = qswc2 / 2. У трьох, показаних на рис. 50, прикладах - а) балка, навантажена рівномірно розподіленим навантаженням, б) балка, навантажена зосередженими силами і в) консоль, навантажена рівномірно розподіленим навантаженням, - епюри Msw врізаються в епюри M. На цих ділянках (заштриховані зони) міцність перетинів не забезпечується. Якщо збільшити qsw. то парабола Msw стане більш крутий, дефіцит міцності зменшиться, але все одно залишиться. Таким чином, одна поперечна арматура, як би багато її ні поставити, міцність похилих перерізів забезпечити не в змозі - потрібна поздовжня арматура.
101. Що таке короткі консолі?
Це консолі, які задовольняють умові l1 # 8804 0,9h0, гдеl1 - розрахунковий виліт, h0 - робоча висота. Зазвичай вони представляють собою бічні виступи у колон, службовці опорами балок, ригелів і тому подібних конструкцій.
102. Як розраховують короткі консолі?
Короткі консолі відчувають вплив великих поперечних сил при відносно невеликих згинальних моментах, тому їх руйнування завжди відбувається не за нормальними, а по похилих перетинах. Досліди показали, що короткі консолі працюють за схемою, близькою до роботи кронштейна. Роль підкоса виконує похила стисла смуга (призма) бетону, а роль розтягнутої зв'язку - розтягнута арматура S (ріс.51). Умова міцності призми виводиться з її геометрії: N # 8804 Nbu. де N = Q / sinq - поздовжнє зусилля в призмі від зовнішнього навантаження, Nbu = 0,8Rbblsupsinqjw - несуча здатність призми. Звідси Q # 8804 0,8Rbblsupsin2q × jw. Тут Q - навантаження на консоль, b - ширина перерізу призми (колони), lsupsinq - висота перетину (lsup - ширина площадки обпирання балок або ригелів), 0,8 - коефіцієнт умов роботи, jw³ 1 коефіцієнт, що враховує вплив поперечної арматури Sw на підвищення призмовою міцності бетону (подібно сіток непрямого армування - см. питання 8).
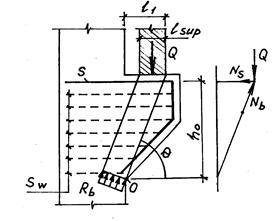
Зусилля в арматурі S можна визначити з суми проекцій сил на горизонтальну вісь, а можна - з суми моментів сил щодо точки спирання підкоса (точка О на рис. 51). Норми рекомендують другий спосіб, тоді As = M / Rsh0. де M = Ql1 (тут плече l1 навмисне взято дещо більше проектної величини з урахуванням можливої нерівномірності опорного тиску балок, неточного їх монтажу і відповідного зміщення рівнодіючої сили Q). Арматура S повинна бути надійно заанкерена по обидві сторони від зони небезпечних перетинів (довжина цієї зони, практично, дорівнює l1)
Якщо умова міцності бетонної призми не виконується, то підвищувати клас бетону не слід - це відіб'ється на вартості всієї колони. Збільшення поперечного армування дає обмежений ефект. Тому найкраще збільшити висоту консолі, що дозволить збільшити кут q. тобто зменшити зусилля в призмі і збільшити площу її поперечного перерізу. Якщо висота перетину консолі свідомо обмежена (архітектурними, технологічними або іншими вимогами), застосовують консолі з жорсткою арматурою.
103. Як розраховують короткі консолі з жорсткою арматурою?
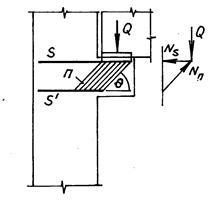
Розраховують так само (рис. 52), як і з гнучкою арматурою, тільки в ролі підкоса використовують похилі сталеві пластини П. з'єднані на зварюванні з арматурними стрижнями - розтягнутими S і конструктивними (слабо стиснутими) S'. Зусилля в пластині і в арматурі знаходять з рішення силового трикутника: Nп = Q / sinq; Ns = Nпcosq. Пластини розраховують без урахування поздовжнього вигину, оскільки бетон перешкоджає втраті стійкості. Розрахунковими також є зварні шви, що з'єднують пластини з арматурою.
3.3. згинальні елементи
104. Що таке епюра матеріалів і для чого її будують?
У згинаного елемента (наприклад, у балки) з постійними по довжині розмірами перетину і армуванням несуча здатність на вигин, рівна Мu = Nbzb + N'szs (її і називають епюр матеріалів, а іноді - епюр арматури), зображується у вигляді прямокутника. Якщо на тій же осі побудувати епюру моментів М від зовнішнього навантаження (наприклад, від q), то видно, що епюри М і Мu зближуються в середині прольоту - тут знаходиться небезпечне перетин, якому відповідає мінімальне відношення Мu / М. Чим ближче до опор, тим більше відношення Мu / M. тим більше запас міцності і тим менш ефективно використовується поздовжня арматура (рис. 53, а). Звідси напрошується просте рішення: доводити до опори не всю арматуру S. а тільки її частину S1. іншу частину S2 обірвати в прольоті. Тоді несуча здатність нормальних перерізів з арматурою S1 зменшиться до величини Мu1 (рис. 53, б).
Очевидно, що точки теоретичного обриву (ТТО) арматури S2 розташовуються на перетині епюри М з епюр Мu1. а відстань а від опори до ТТО визначається з рівності Мu1 = M, де для даної схеми навантаження М = 0,5qa (l-a). Фактично ж арматура S2 повинна бути заведена за ТТО на довжину не менше w (див. Питання 105).
Слід також пам'ятати, що до опори (точніше, за грань опори) має бути доведено не менше 2-х стержнів арматури S1 (при ширині елемента менше 150 мм допускається доводити один стрижень).