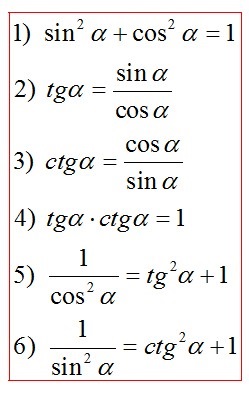
Парність, непарність тригонометричних функцій
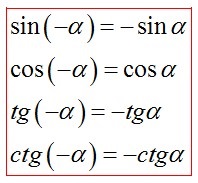
формули приведення
Це співвідношення, за допомогою яких значення тригонометричних функцій аргументів і ін. Виражаються через значення.
Правила перетворення:
1) Якщо аргумент містить, де n - непарне натуральне число, то функція змінюється на "конфункцію", тобто синус на косинус, тангенс на котангенс і навпаки. Якщо n - парне натуральне число, то назва функції не змінюється.
2) Визначаємо знак ( "+" або "-") значення початкової функції. Перетворене вираз зберігає знак свого батька.
Формули додавання і віднімання
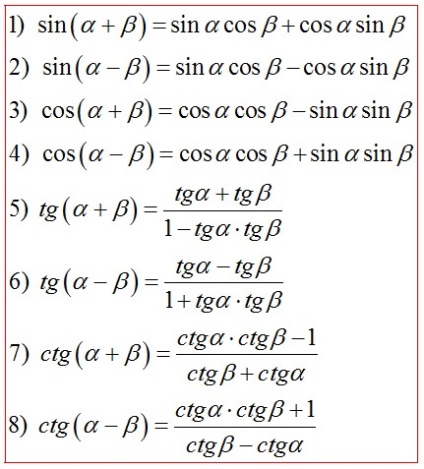
Формули подвійного кута
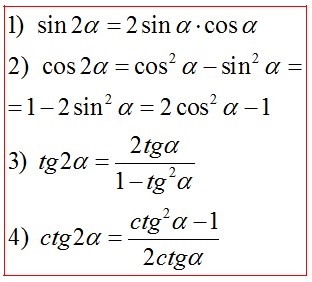
Формули перетворення суми і різниці в твір
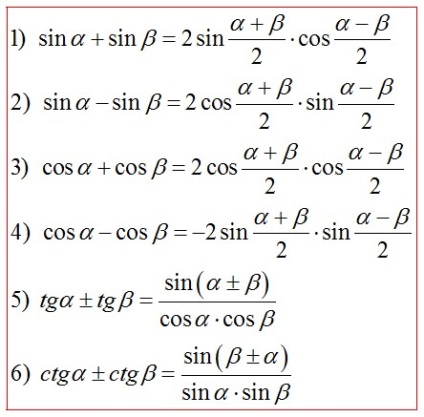
Формули половинного аргументу
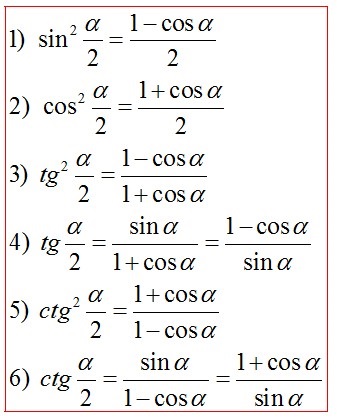
Формули потрійного кута *
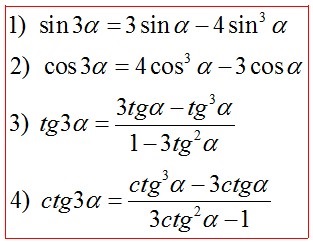
Формули перетворення добутку в суму (різницю) *

Універсальна підстановка через тангенс половинного аргументу *
