У минулій лабораторній роботі були розглянуті основні питання, пов'язані з дискретними відображеннями і побудовою павутинних діаграм. Біфуркаційних діаграма є розвитком павутинної діаграми, тому що дозволяє досліджувати режими, в яких знаходиться система, при завданні деякого діапазону параметра. Основні принципи побудови бифуркационной діаграми також були приведені в описі попередньої лабораторної роботи.
Наприклад, візьмемо відому логістичну функцію і поспостерігаємо весь каскад біфуркацій, які відбуваються з системою при плавній зміні параметраλ. Для цього, виберемо якусь початкове значеніеx і виконаємо над ним 100-200 ітерацій відображення логістичної функції. Потім відкладемо значення наступних 100-200 ітерацій по вертикальній осі, а значення параметраλ. при якому проводилися обчислення, - по горизонтальній. За осіλ пройдемо відрізок від 2,9 до 4 з невеликим інтервалом, наприклад 0,01. Отримане безліч називається бифуркационной діаграмою логістичної функції. В результаті обчислень повинна вийти наступна картина.
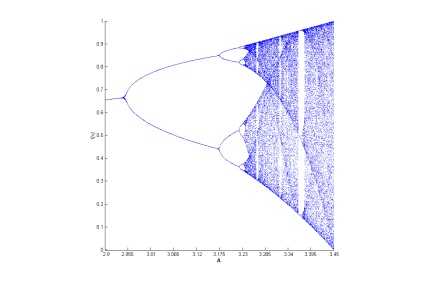
Мал. 5.1. Біфуркаційних діаграма логістичної функції.
Порядок побудови бифуркационной діаграми
1. Вибираємо початкове значення x (наприклад, x = 0.5) і початкове значеніеλ.
2. Проводимо 200 ітерацій заданого відображення.
3. Запам'ятовуємо або відображаємо значення наступних 100 ітерацій відображення.
4. Збільшуємо значення λ на заданий крок і повторюємо процедуру обчислень.
Завдання на лабораторну роботу
1. Ознайомитися з теоретичним введенням до лабораторної роботи.
2. За допомогою програми Chaos (в средеMatLAB) побудувати біфуркаційні діаграми нелінійних дискретних відображень у відповідності зі своїм варіантом при різних значеннях параметраλ. Здійснюється варіант повинен відповідати варіанту попередньої роботи.
3. Написати функцію, що дозволяє побудувати біфуркаційні діаграми для заданого нелінійного дискретного відображення.
4. Порівняти отримані результати з результатами програми Chaos.