Початковий курс математики, досліджуваний в I-IV класах школи, є органічною частиною шкільного курсу математики. Це означає, що курс математики для V-X класів - продовження початкового курсу, а початковий курс - його вихідна база. Відповідно до цього початковий курс математики включає арифметику цілих невід'ємних чисел і основних величин, елементи алгебри і геометрії.
Початковий курс математики має свої особливості побудови.
Такий зв'язок дає можливість, з одного боку, раніше долучити дітей до ідей алгебри і геометрії і з іншого - досягти більш високого рівня засвоєння молодшими школярами арифметичних знань.
Арифметичний матеріал вводиться концентрично. Спочатку вивчається нумерація чисел першого десятка, які не підлягають десятичному розчленування, вводяться цифри для запису цих чисел, вивчаються дії додавання і віднімання. Потім розглядається нумерація чисел в межах 100, розкривається поняття розряду, позиційний принцип запису чисел, які підлягають десятичному розчленування, вивчається додавання і віднімання двозначних чисел, вводяться два нових арифметичних дії: множення і ділення. Далі вивчається нумерація чисел в межах 1000. Тут розглядаються три розряди (одиниці, десятки, сотні), що становлять основу нумерації багатозначних чисел, узагальнюються знання про арифметичні дії, вводяться прийоми письмового додавання і віднімання. Нарешті, вивчається нумерація багатозначних чисел, розглядається поняття класу, узагальнюється знання принципу помісного значення цифр, вивчаються прийоми письмових обчислень. Таким чином, в курсі виділені чотири концентрації: десяток, сотня, тисяча, багатозначні числа. Одночасно і в тісному зв'язку з розглядом нумерації і арифметичних дій вивчаються інші питання: величини, дробу, алгебраїчний і геометричний матеріал.
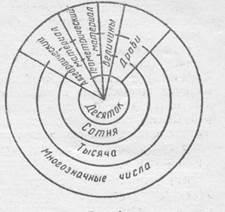
Схематично розташування матеріалу зображено на малюнку.
Виділення саме таких концентров пояснюється особливостями десяткової системи числення і обчислювальних прийомів: в кожному концентре розкриваються нові питання, пов'язані з системою числення і арифметичними діями. Як показав досвід, концентричне розташування матеріалу відповідає можливостям молодших школярів: навчання математики починається з невеликої області чисел, доступною дітям і відомої їм до школи; ця область чисел поступово розширюється, і поступово вводяться нові поняття; при такій побудові курсу забезпечується систематичне повторення і разом з тим поглиблення вивченого, так як отримані раніше знання, вміння і навички знаходять застосування в новій області чисел. Все це сприяє кращому засвоєнню курсу.
Математичні поняття, властивості, закономірності розкриваються в курсі в їх взаємозв'язку. Це не тільки зв'язок між арифметичним, алгебраїчним і геометричним матеріалом, але і так звані внутрішні зв'язки між різними поняттями курсу, властивостями, закономірностями. Так, при вивченні арифметичних дій розкриваються їх властивості, зв'язки і залежності між їх компонентами і результатами. Це дає можливість глибше розкрити поняття арифметичних дій, збагатити дітей функціональними уявленнями. Така побудова забезпечує більш глибоке засвоєння курсу, так як учні опановуватимуть не тільки окремими питаннями курсу, але одночасно і зв'язками між ними.
Арифметичний матеріал включає нумерацію цілих невід'ємних чисел і арифметичні дії над ними, відомості про величини, їх вимірі і діях над ними, поняття про дроби.
Вивчення цього матеріалу має привести учнів до засвоєння системи математичних понять, а також до оволодіння міцними і усвідомленими вміннями і навичками.
Число нуль трактується в початковому курсі як кількісна характеристика класу порожніх множин. Включення в початковий курс математики числа і цифри нуль дозволяє розширити числову область і створити належні умови для оволодіння учнями областю цілих невід'ємних чисел. Нуль як число і як цифра вводиться в I класі. Спочатку нуль розглядається як цифра, що позначає на лінійці початок отмеривания, потім вводиться число нуль при відніманні виду: 2-2, 3 - 3, що відповідає правильному тлумачення сутності цього нового числа як кількісної характеристики класу порожніх множин. Далі нуль виступає як компонент дій першого ступеня: 5 + 0, 0 + 9, 8-0, 0 + 0, О-О, а при вивченні дій множення і ділення (II клас) як компонент цих дій: 0-4, 3 -0, 0-0, 0: 4. Тут же розглядається неможливість поділу на нуль. Цифра нуль використовується для позначення відсутності одиниць будь-якого розряду в запису числа (70, 30000, 204).
У початкових класах дається наочне уявлення про дроби. У II класі вводиться поняття частки як однієї з рівних частин цілого (кола, шматка шпагату.), Дається запис часткою. Оскільки суть поняття частки дуже яскраво розкривається при вирішенні задач на знаходження частки від числа і числа за його частці, то ці завдання включені в курс, що вивчається в II класі. У III класі вводиться дріб як сукупність часток, запис дробу, перетворення і порівняння дробів на завдання на знаходження дробу числа.
Поняття про систему числення розкривається при концентричному побудові курсу поступово, в процесі вивчення нумерації натуральних чисел і арифметичних дій над ними. При цьому поняття розряду, класу, розрядної і класної одиниці, розрядного числа, як уже вказувалося, знаходить свій розвиток від концентра до концентру, т. Е. Поступово вводяться нові розряди і класи, їх назву і в зв'язку з цим розглядаються освіту, назва, запис і читання чисел, їх десятковий склад.
Арифметичні дії займають центральне місце в початковому курсі математики. Це складний і багатогранний питання. Він включає розкриття конкретного змісту арифметичних дій, властивостей дій, зв'язків і залежностей між компонентами і результатами дій і між самими діями, а також формування обчислювальних умінь і навичок, умінь вирішувати арифметичні завдання.
Як і інші математичні поняття, кожне арифметична дія розкривається на конкретній основі в процесі виконання операцій над множинами: додавання - на основі операції об'єднання множин, які не мають спільних елементів, віднімання - на основі операції видалення частини безлічі (підмножини), множення - на основі операції об'єднання множин однаковою чисельності та розподіл - на основі операції розбиття множини на ряд рівночисельний непересічних множин. Такий підхід дозволяє скористатися досвідом дітей і створити наочну основу формованого знання. Одночасно з розкриттям конкретного сенсу кожного арифметичного дії вводиться відповідна символіка (знаки дій) і термінологія: назва дії, назва компонентів і результатів дії. Тут же починається робота над поняттям математичного виразу, спочатку розглядаються найпростіші вирази виду: 7 + 3, а пізніше більш складні види: 9-(2 + 3).
Початковий курс математики включає ряд властивостей арифметичних дій. Це переместительное властивість додавання і множення, властивості додавання числа до суми, віднімання числа від суми, додавання суми до числа, віднімання суми з числа, додавання суми до суми, віднімання суми від суми, множення числа на суму і суми на число, ділення суми на число, множення числа на добуток, ділення числа на добуток.
Кожне з названих властивостей розкривається на основі практичних операцій над множинами або над числами, в результаті чого учні повинні прийти до узагальнення. Для засвоєння властивостей в курсі передбачається система спеціальних вправ, але головна сфера застосування властивостей - це розкриття на їх основі обчислювальних прийомів. Наприклад, уже в Iклассе після вивчення переместітельного властивості складання вводиться прийом перестановки доданків для випадків виду: 2 + 6; нагоди 54 - 20 передує розгляд різних способів віднімання числа із суми, на основі чого розкривається обчислювальний прийом:
54-20 = (50 + 4) -20 = (50-20) +4 = 34.
Спираючись на конкретний зміст арифметичних дій, їх властивості, зв'язки і залежності між результатами і компонентами дій, а також десятковий склад чисел, розкриваються прийоми усних і письмових обчислень. Такий підхід до вивчення прийомів обчислень забезпечує, з одного боку, формування усвідомлених умінь і навичок, так як учні зможуть обґрунтувати будь-обчислювальний прийом, а з іншого боку, при такій системі краще засвоюються властивості дій і інші питання курсу.
Одночасно з вивченням властивостей арифметичних дій і відповідних прийомів обчислень розкриваються на основі операцій над множинами або над числами зв'язку між компонентами і результатами арифметичних дій (наприклад, якщо з суми відняти один з доданків, то вийде інше доданок), ведуться спостереження за зміною результатів арифметичних дій в залежності від зміни одного з компонентів (наприклад, якщо одна з складових збільшити на кілька одиниць, а інше залишити без зміни, то сума увеличи ся на стільки ж одиниць).
У початковому курсі математики передбачається система вправ, спрямованих на вироблення в учнів обчислювальних навичок. Це тренувальні вправи різного характеру: рішення окремих прикладів, заповнення таблиць, підстановка числових значень букв і знаходження значень отриманих виразів. У формуванні навичок передбачається різна ступінь їх автоматизації: навички додавання і множення табличних випадків і зворотні по відношенню до них випадки віднімання і ділення повинні бути доведені до повного автоматизму (так, учні повинні швидко і правильно відтворювати, що 3 + 8 = 11, 7x6 = 42, 12 - 5 = 7, 56: 8 = 7). Автоматизується і виконання окремих операцій; наприклад, при додаванні чисел 18 і 7 швидко виконуються операції: 8 + 7 = 15, 10 + 15 = 25 або 7 = 2 + 5, 18 + 2 = 20, 20 + 5 = 25.
Всі названі питання, що відносяться до арифметичних дій, розглядаються в тісному взаємозв'язку один з одним.
У зв'язку з вивченням арифметичного матеріалу вводяться елементи алгебри: на конкретній основі розкриваються поняття рівності, нерівності, рівняння, змінної.
Починаючи з I класу розглядаються числові рівності і нерівності
3 = 3, 5 = 1 + 4, 3<4, 7+2>7, 9-3<9-2 и т. п. Их изучение непосредственно связывается с изучением арифметического материала и помогает более глубоко раскрыть его. Здесь же рассматриваются уравнения сначала вида: х + 6 = 9, 10—х=2.. а позднее, начиная соIIкласса, вида: (48 ++х)— 24 = 36. Решение уравнений выполняется на основе связи между компонентами и результатами арифметических действий, а также способом подбора. Наряду с решением уравнений ведется обучение решению задач с помощью составления уравнений. ВоIIклассе вводится буква как символ для обозначения переменной. В связи с этим рассматриваются выражения с переменной(а + Ь, 20 —с и др.) и неравенства с переменной 9 —с<5), значения переменной в которых находится способом подбора.
Геометричний матеріал служить головним чином цілям ознайомлення з найпростішими геометричними фігурами і розвитку просторових уявлень школярів. Тому в початковий курс математики, починаючи з I класу, включені геометричні фігури: прямі, криві і ламані лінії, точка, відрізок прямої, багатокутники (трикутник, чотирикутник.) І їх елементи (вершини, сторони, кути), прямий кут, прямокутник ( квадрат), окружність, коло, центр і радіус кола. Учні повинні навчитися розрізняти ці фігури, називати їх і виконувати найпростіші побудови на картатій папері. Крім того, вони повинні оволодіти вмінням знаходити довжину відрізка (I клас), довжину ламаної і периметр багатокутника (II клас), площа геометричної фігури (III клас) .Курс математики передбачає різноманітні завдання геометричного характеру, спрямовані на формування просторових уявлень учнів. Всі питання геометрії розкриваються на наочної основі.
У тісному зв'язку з вивченням арифметичного, алгебраїчного і геометричного матеріалу розкривається поняття величини і ідея вимірювання величин. Ознайомлення з такими величинами, як довжина, маса, час, ємність, площа, з одиницями їх вимірювання і з вимірюванням величин виконується практично і тісно пов'язується з формуванням поняття числа, десяткової системи числення і арифметичних дій, а також з формуванням поняття геометричної фігури. Внаслідок такого зв'язку стає можливим вести навчання, спираючись на наочні образи, пов'язуючи навчання з практичною діяльністю дітей.