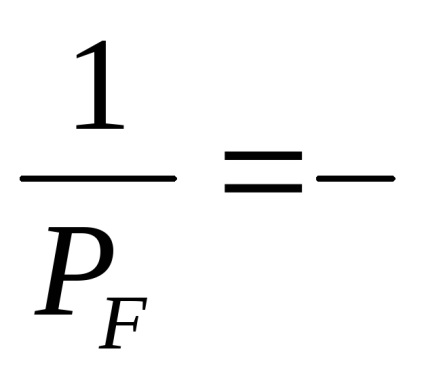При зрівнюванні тріангуляції в рівняннях поправок напрямків крім правок до наближених значень координат присутні поправки в орієнтують кути станцій

де С і А матриці коефіцієнтів при векторах поправок в орієнтують кути


Їй буде відповідати система нормальних рівнянь
де - вагова матриця виміряних напрямків.
Застосовуючи метод підстановки і виключаючи

Цю перетворену систему можна одержати й іншим шляхом.
Нехай виміряним на станції i напрямками відповідають наступні рівняння поправок
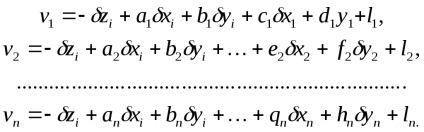
Їм буде відповідати наступна система нормальних рівнянь:
Якщо з першого рівняння системи (134) відняти
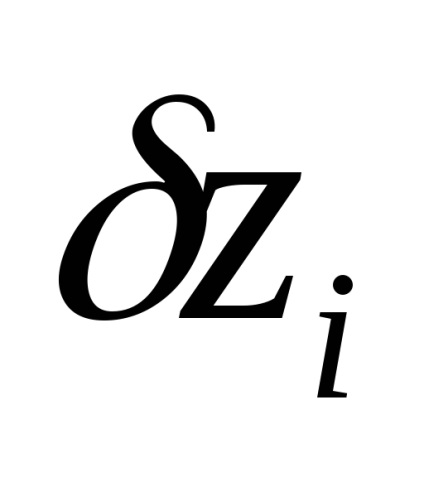
і підставити його в інші, то отримаємо еквівалентну систему
Виходячи з неї легко помітити, що матрицю нормальних рівнянь можна складати на основі існуючих рівнянь поправок з додаванням на кожній станції так званого сумарного рівняння
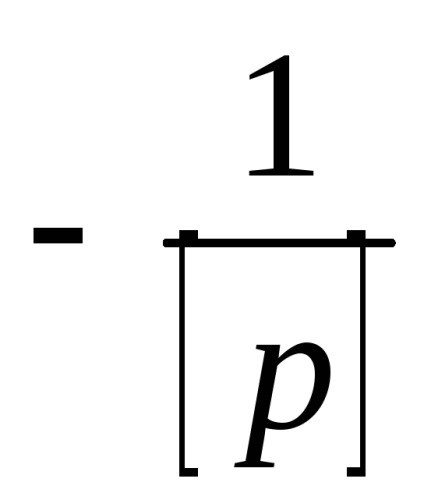
Приклад зрівнювання геодезичної мережі параметричним способом
Зрівняти параметричних способом геодезичну мережу, наведену на рис. 21 в прикладі зрівнювання коррелатним способом.
Наближені координати пунктів D і Е прийняти наступними
Відзначимо, що вони можуть бути знайдені за результатами вимірювань в геодезичної мережі.
Спочатку для обчислення вільних членів рівнянь поправок необхідно за значеннями наближених координат пунктів, що визначаються і за координатами вихідних обчислити дирекційні кути і довжини сторін з точністю, відповідної прийнятим наближеним координатами. Для Цього вирішуються зворотні геодезичні завдання за формулами
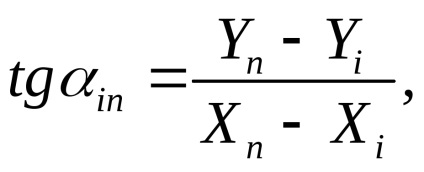
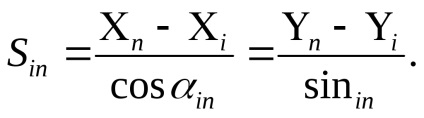
де i, n- номера пунктів.
Після того, як точно обчислені довжини сторін і кути дирекцій за попередніми координатами, обчислюються вільні члени рівнянь поправок (таблиця 15). У цій же таблиці обчислюються коефіцієнти
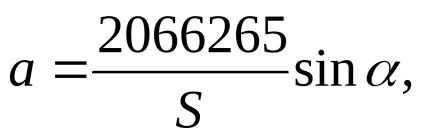
необхідні для складання матриці коефіцієнтів рівнянь поправок.
Відповідно до (115) і (137) рівняння поправок для кожного виміряного напрямку матимуть вигляд
а для виміряної боку вид (108).
Система рівнянь поправок для всієї мережі приведена в таблиці 16.
Там же для кожної станції складені і сумарні рівняння виду (136).
Система нормальних рівнянь
представлена в таблиці 17.
Система нормальних рівнянь
У таблиці 17 наведено лише верхній трикутник матриці нормальних рівнянь
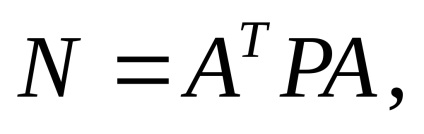
вектор вільних членів
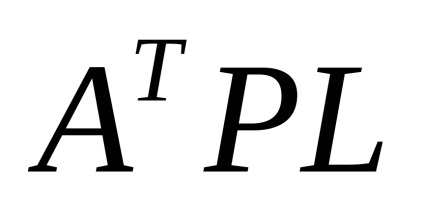
Система нормальних рівнянь тут складається так само, як і система нормальних рівнянь коррелат. Але в даному випадку виконується множення відповідних стовпців на ваги вимірювань, а не їх зворотних величини, як в коррелатном способі.
Рішення нормальних рівнянь за схемою Гаусса наведено в таблиці 18.
За отриманими поправкам до координат пунктів, що визначаються Dи Е і їх наближеним координатам обчислюються остаточні значення

На основі (135) обчислюється поправка в орієнтує кут для кожної станції.
Рішення нормальних рівнянь за схемою Гаусса
З урахуванням цієї поправки і значень поправок в наближені координати пунктів, що визначаються на основі рівняння поправок напрямків (138) обчислюються поправки напрямків. Поправки в виміряні сторони обчислюються простий підстановкою поправок координат в рівняння поправок сторін (108). Їх обчислення наводяться в таблиці 16.
Отримані поправки з точністю обчислень повинні збігатися з поправками, знайденими коррелатним способом зрівнювання.
Обчислення середньої квадратичної помилки одиниці ваги також виконується за формулою (94). У загальному випадку в параметричному способі число надлишкових вимірювань визначається за формулою
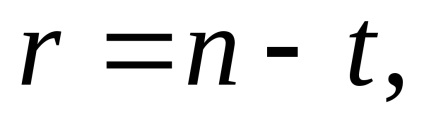
де n - число рівнянь поправок, t - число невідомих параметрів. При зрівнюванні напрямків число t обчислюється за формулою
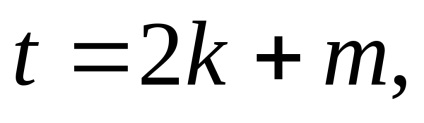
де k - число пунктів, що визначаються, m - число станцій з яких вимірювалися напрямку. Якщо на кожному пункті напрямки вимірювалися лише один раз, то число m дорівнює числу всіх пунктів, включаючи і вихідні. Це число дорівнює числу всіх орієнтують кутів, тобто числу вимірюваних пучків напрямків.
Значення середньоквадратичної помилки одиниці ваги є оцінкою стандарту в (128). Далі за формулою (128) можна обчислити оцінку точності будь-якої функції після зрівнювання. В параметричному способі зручно оцінювати точність визначених пунктів за формулою (131). При цьому необхідно звернути матрицю нормальних рівнянь N.
Її звернення можна здійснити різними способами. Найбільш зручний з них спосіб модифікованих Жорданових винятків.
Суть його полягає в наступному:
1) У вихідній матриці вибирається дозволяє елемент
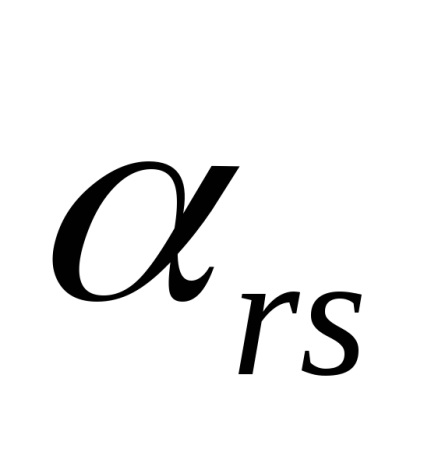
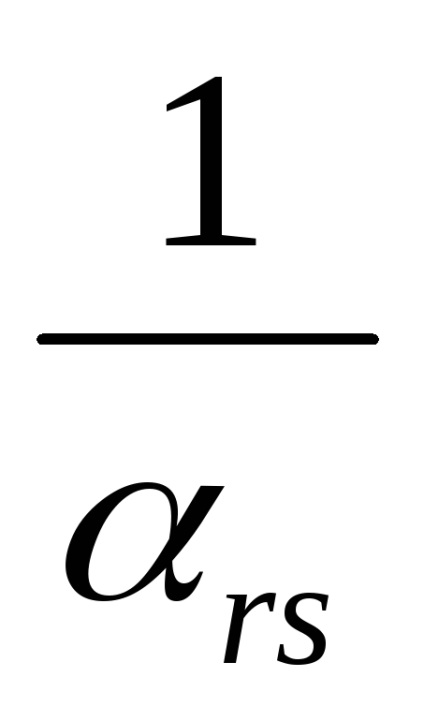
2) Інші елементи роздільної рядка r діляться на дозволяючий елемент.
3) Інші елементи дозволяє стовпця S діляться на дозволяючий елемент і змінюють на протилежні.
4) інші елементи обчислюються за формулою:
Обчислення доцільно виконувати з утримуванням двох значущих цифр після коми.
На першому кроці Жорданових винятків як дозволяє приймається діагональний елемент 4,17.
В результаті вийде матриця
На другому кроці що дозволяє буде другий перетворений діагональний елемент матриці (141), тобто 7,90.
На третьому кроці що дозволяє береться діагональний елемент матриці 9142). 9,75.
На четвертому кроці, тобто останньому, що дозволяє буде елемент 8,13.
Остаточний результат представиться у вигляді матриці
яка буде зворотної матриці (139).
Контролем правильності звернення є рівність одиничної матриці твори матриць (139) і (144) з точністю 0,1. Крім того при переході з одного кроку Жорданових винятків до іншого необхідно стежити за симетричністю утворюваних матриць. Лише в роздільної рядку зліва і в дозвільному стовпці зверху від дозволяє елемента матриці розрізняються лише знаками.
І підсумку згідно з формулою (131) знайдемо
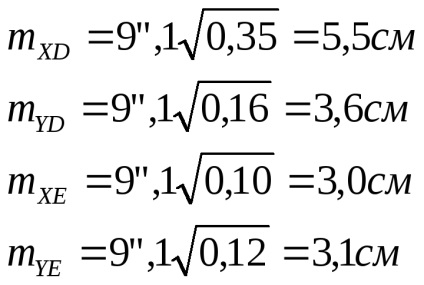
Помилки загального положення пунктів D і Е будуть
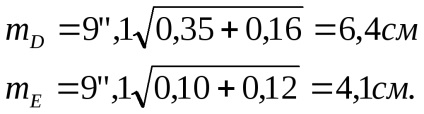
Використовуючи матрицю (144) і стовпець А Т РL таблиці 17 по формулі (130) можна знайти поправки в наближені координати пунктів, що визначаються. вони будуть рівними обчисленими в таблиці 18 при вирішенні нормальних рівнянь за схемою Гаусса.
Оцінку точності окремої функції можна зробити і за формулою Гаусса. При цьому складається вагова функція по визначеним параметрам
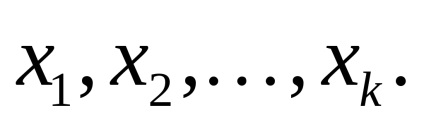
де
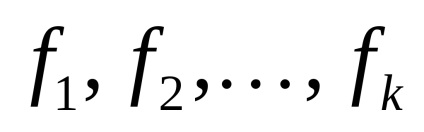
У цьому завданню такими параметрами є поправки в наближені координати пунктів, що визначаються, тобто
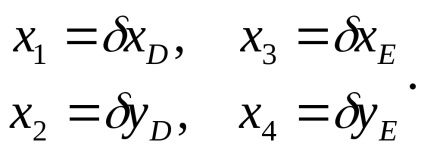
Зворотна вага цієї функції дорівнює величині