При викладі теорії початкової остійності судна було відзначено, що допущення про лінійну залежність відновлюючого моменту від кута нахилу справедливо тільки для малих кутів нахилу судна, за межами яких плече остійності і відновлює момент вже не можуть визначатися метацентричної формулами. Тому для характеристики остійності за межами малих кутів нахилу доводиться вдаватися до апарату теорії остійності на великих кутах нахилу. При цьому будемо розглядати тільки остійність при великих кутах крену, оскільки великі кути дифферента у неушкодженого судна практично не виникають.
Говорячи про способі судна в поперечній площині слід мати на увазі, що внаслідок несиметрії судна відносно площини мидель-шпангоута центр величини виходить з площини способу і утворюється друга складова повного моменту сил ваги і плавучості - т.зв. дериваційний момент, діючий в поздовжній площині. Однак істотна відмінність між повним і відновлює моментами, навіть при великих кутах крену, виявляється лише в деяких випадках способу пошкодженого судна із затопленими відсіками. Для неушкодженого судна з достатньою для практичних цілей точністю можна вважати, що остійність судна повністю визначається відновлює моментом (чинним в площині способу) і обмежитися, тому, розглядом залежностей, що виражають його величину при нахилі судна.
Прирассмотрении початкової остійності були прийняті наступні основні допущення:
При крен судна переміщення центру величини відбувається по дузі кола;
Поперечний метацентр знаходиться в точці, яка є центром цієї окружності і не змінює свого положення при наклонениях;
Значення поперечного метацентричної радіусу залишається незмінним;
Равнооб'емние ватерлінії перетинаються по прямій, що проходить через центр ваги площі ватерлінії, розташований в діаметральній площині судна.
Однак в процесі експлуатації судна часто виникають способу на великі кути крену. У цих випадках застосування перерахованих припущень призводить до невірних результатів. Тому і була розроблена теорія остійності судна при великих нахилах.
При великих кутах нахилу судно не можна вважати Прямостінні в межах зміни форми підводного обсягу: симетрія входить івиходящей частин площі похилій ватерлінії значно порушується, що призводить до зміщення осі перетину двох равнооб'емние ватерліній. Переміщення центру величини при великих кутах крену відбувається вже не по дузі кола, а по кривій змінної кривизни. Це рівнозначно тому, що поперечний метацентр не залишається в постійній точці m на діаметральноїплощині, як це було при малих кутах крену, а зміщується в нову точку m. Отже, і відстань між метацентром і центром величини - поперечний метацентричної радіус - є змінною величиною. Положення центра ваги площі діючої ватерлінії буде визначатися тільки шляхом обчислення фактичного положення равнооб'емние ватерліній. Т.ч. змінність величини метацентричної радіуса можна пояснити і тим, що при крен судна форма площі діючої ватерлінії змінюється, її поздовжня центральна вісь способу зміщується щодо діаметральної площині і, отже, значення моменту інерції Ixx буде різним для кожної діючої ватерлінії.
Зі сказаного випливає, що метацентрическая висота вже не може служити критерієм поперечної остійності. З цих міркувань, вирішуючи питання остійності при великих кутах крену, не можна користуватися метацентрической формулою поперечної остійності і всіма отриманими на її підставі формулами, в які входить значення поперечної метацентрической висоти.
Під остойчивостью судна розуміється його здатність чинити опір крениться момент. Але кренить судно, власне, крениться момент, а сопротівляетсяемувосстанавлівающій момент. Тому що відновлює моментом і слід вимірювати остійність судна в цьому випадку.
Мірою статичної остійності судна при великих кутах крену буде відновлює момент, рівний:
Основне завдання розрахунку остійності при великих кутах крену зводиться до визначення плеча lст відновлює моменту в залежності від кута нахилу.
При поперечному равнооб'емние способі на кут. на величину якого не накладаються які-небудь обмеження, центр ваги судна не змінить свого положення, а центр величини переміститься в бік нахилу. Метацентр також займе нове положення (Рис.3.1) Діючі на судно сили ваги і плавучості спрямовані по нормалям до ватерлінії і утворюють пару сил з плечем GK, значення якого вже не можна виразити через поперечну метацентричної висоту. Згідно рис.3.1 відновлює момент можна подати як різницю моментів сили плавучості і сили ваги D щодо початкового положення центру величини С Плече цієї пари GK =. як і раніше, назвемо плечем статичної остійності, а момент D - відновлює моментом
Відрізок l називають плечем остійності форми, так як при цьому вазі судна Р і вугіллі крену його значення залежить тільки від координат центру величини, що визначаються формою підводного обсягу судна. Відрізок l називають плечем остійності ваги, так як при цьому вугіллі крену його довжина залежить тільки від піднесення центру ваги над центром величини. Відповідно момент називають моментом остійності форми, а момент - пліч-о-остійності ваги.
Іноді плечем остійності форми називають довжину перпендикуляра OR, опущеного на лінію дії сили плавучості з початку координат.
В цьому випадку плече статичної остійності ваги буде, а плече статичної остійності виразиться залежністю
Поділ плеча остійності на дві складові l і l полегшує його обчислення, оскільки плечі форми можуть бути обчислені заздалегідь (в конструкторському бюро) і представлені у вигляді кривих в залежності від водотоннажності судна і кутів крену, а на судні для кожного кута крену необхідно тільки визначити величину а піднесення ЦТ над ЦВ при даному стані навантаження судна.
Діаграма статичної остійності.
Плече відновлює моменту l і сам момент Мв мають геометричну інтерпретацію у вигляді діаграми статичної остійності (ДСО) (Рис.3.2). ДСО - це графічна залежність плеча відновлює моментаl (# 952;) або самого моменту Мв = від кута крену # 952; .
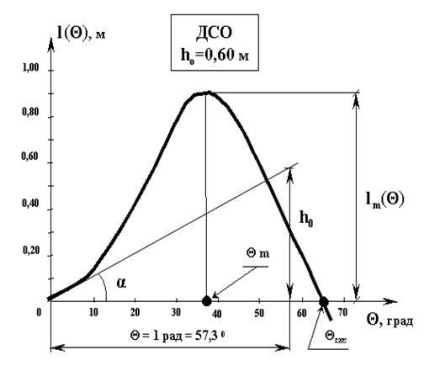
Цей графік, як правило, зображують для крену судна тільки на правий борт, оскільки вся картина при крен на лівий борт для симетричного судна відрізняється тільки знаком моменту Мв (# 952;).
Значення ДСО в теорії остійності дуже велике: це не тільки графічна залежність Мв (# 952;); ДСО містить в собі вичерпну інформацію про стан завантаження судна з точки зору остійності. ДСО судна дозволяє вирішувати багато практичні завдання в даному рейсі і є звітним документом для можливості почати завантаження судна і відправку його в рейс.
Діаграма статичної остійності має вигляд кривої з яскраво вираженим максимумом. На ній можна відзначити три точки, характерні для неушкодженого судна, що володіє позитивною остойчивостью: точку О (початок координат), що визначає положення стійкої рівноваги; точку. де плече статичної остійності і відновлює момент мають максимальні значення, і точку. визначальну т.зв. кут заходу діаграми.
Рівновага накренившись судна настає при рівності крениться Мкр і відновлює моментів Мв. Щоб скористатися діаграмою статичної остійності для визначення кута нахилу, який виник під дією заданого крениться моменту Мкр, необхідно знайти плече крениться моменту
І умова рівноваги судна можна записати у вигляді lкр = lв.
На діаграмі статичної остійності в точці перетину відновлює момент дорівнює крениться і, отже, судно знаходиться в рівновазі в похилому положенні (див. Рис.3.3).
Але таких точок перетину на ДСО буде дві. Розі статичного крену (положення стійкої рівноваги) буде відповідати точка А.
Відхилення від нього в будь-яку сторону на малий кут веде до виникнення моменту. прагне повернути судно в вихідне рівноважний стан. Інша картина спостерігається в точці В - найменше відхилення від неї на кут негайно призводить до перекидання судна, оскільки в області> крениться момент стає більше, що відновлює; при відхиленні на кут <0 наоборот,> і під дією різниці моментів судно буде йти з точки В в сторону зменшення кута нахилу до тих пір, поки в точці А знову не відновиться рівновага, тепер уже стійке. Неважко переконатися, що всі крапки рівноважного положення накрененного судна припадають на висхідну гілку ДСО, відповідають його стійкого рівноваги, і, навпаки, точки низхідній гілці ДСО - відповідають нестійкого рівноваги. Отже, у міру збільшення статичного крениться моменту кут крену буде рости і перекидання відбудеться, коли крениться момент трохи - трохи перевищить максимальний відновлює момент, а кут перекидання буде дорівнює куту максимуму ДСО.
Діаграма статичної остійності будується для конкретного судна і відповідає певним водотоннажності V і положенню центра ваги по висоті Zg. Якщо у даного судна зміниться водотоннажність або аппликата центру ваги, то ДСО придбає інший вигляд. Ця обставина завжди треба мати на увазі. Кожне судно повинно бути забезпечене комплектом діаграм статичної остійності, що характеризують його остійність при найбільш часто зустрічаються варіантах навантаження. ДСО відрізняються великою різноманітністю форм кривих, але всі вони мають деякими загальними властивостями:
1. Початкова ділянка ДСО є прямою похилу лінію. Дійсно, при малих кутах крену початкова ділянка діаграми повинен бути прямим, що можна довести прирівнявши дві формули, що відновлює моменти: метацентричної формулу поперечної остійності, яка застосовується тільки для малих кутів крену, і формулу відновлює моменту, справедливу для будь-яких кутів крену, тобто = Dh і = Dlст, звідки lст = h.
При малих кутах крену поперечна метацентрическая висота h - постійна величина, тому залежність між плечем статичної остійності і кутом крену при малих значеннях останнього є лінійної і зображується прямою лінією.
2.Отрезок перпендикуляра, відновленого з точки на осі абсцис, що знаходиться на відстані одного радіана від початку осей координат, до точки перетину його з початкової дотичній до кривої, визначає на ДСО початкову поперечну метацентричної висоту h.
tg. але lст = h; тоді tg (3.5)
Однак графічно визначати метацентричної висоту по ДСО не рекомендується, тому що проведення дотичної до кривої не може бути виконано з необхідною точністю. Зазначене властивість ДСО застосовують головним чином для контролю її початкового ділянки, коли відома поперечна метацентрическая висота.
У загальному вигляді це властивість ДСО формулюється так: кутовий коефіцієнт дотичної до діаграми в будь-якій точці пропорційний т.зв. «Узагальненої» метацентрической висоті, що відповідає тому чи іншому значенню кута крену, який визначається абсцисою точки дотику.
Аналітично ці властивості виражаються похідною від плеча остійності по куту нахилу, тобто узагальнена метацентрическая висота виражається у вигляді:
Випливають звідси властивості ДСО такі:
-.Для максимуму діаграми узагальнена метацентрическая висота дорівнює нулю
-. Кривизна початкової гілки діаграми дозволяє судити про початкову остійності судна
3.Восходящая частина кривої діаграми статичної остійності характеризує стійке положення рівноваги судна, а спадна - нестійке.
- ДСО конкретного судна залежить тільки від взаємного розташування центру ваги судна G і початкового поперечного метацентра m (або значення метацентрической висоти h0) і водотоннажності Р (або опади dср) і враховує наявність рідких вантажів і запасів за допомогою спеціальних поправок,
- форма корпусу конкретного судна проявляється в ДЗГ через плече l (# 952;), жорстко пов'язане з формою обводів корпусу, яке відображає зміщення центру величини С в бік вхідного в воду борту при накрененіі судна ,.
- метацентрическая висота h0. обчислена з урахуванням впливу рідких вантажів і запасів (див. нижче), проявляється на ДСО як тангенс кута нахилу дотичної до ДСО в точці # 952; = 0 (Рис.3.4), тобто .:
Для підтвердження правильності побудови ДСО на ній роблять побудову: відкладають кут # 952; = 1 рад (57,3 0) і будують трикутник з гіпотенузою, дотичній до ДСО при # 952; = 0, і горизонтальним катетом # 952; = 57,3 0. Вертикальний (протилежні) катет повинен виявитися рівним метацентрической висоті h0 в масштабі осі l (м).
- ніякі дії не можуть змінити виду ДСО, крім зміни величин вихідних параметрів h0 і Р. оскільки ДСО відображає в якомусь сенсі незмінну форму корпусу судна за допомогою величини l (# 952;);
- метацентрическая висота h0 фактично визначає вид і протяжність ДСО.
кут крену # 952; = # 952; 3. при якому графік ДСО перетинає вісь абсцис, називається кутом заходу ДЗГ. кут заходу # 952; 3 визначає тільки те значення кута крену, при якому сила ваги і сила плавучості будуть діяти уздовж однієї прямої і l ( # 952; 3) = 0. Судити про перекиданні судна при крені
# 952; = # 952; 3 НЕ буде вірним, оскільки перекидання судна починається набагато раніше - незабаром після подолання максимальної точки ДСО. Точка максимуму ДСО (l = lm (# 952; m)) свідчить лише про максимальному видаленні сили ваги від сили підтримки. Однак, максимальне плече lm і кут максимуму # 952; m є важливими величинами при контролі остійності і підлягають перевірці на відповідність відповідним нормативам.
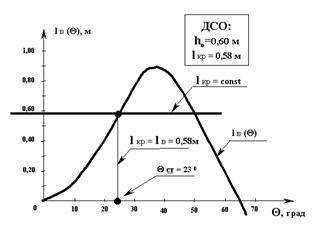
Рис.3.5 Взаємодія крениться і відновлює моментів.
Діаграма статичної остійності відображає можливість судна створювати відновлює момент при нахилі судна. Її вигляд має строго конкретний характер, відповідний параметрам завантаження судна тільки в даному рейсі (Р = Рi. H0 = h0i). Судоводитель, що займається на судні питаннями планування рейсу навантаження і розрахунками остійності, зобов'язаний побудувати конкретну ДСО для двох станів судна в майбутньому рейсі: з незмінним початковим розташуванням вантажу і при 100% і при 10% суднових запасів.
Щоб мати можливість будувати діаграми статичної остійності при різних поєднаннях водотоннажності і метацентрической висоти, користуються допоміжними графічними матеріалами, наявними в судновий документації по проекту цього судна, наприклад, пантокаренамі, або універсальної діаграмою статичної остійності.