Початкову позицію можна розкласти багатьма способами. всього існує
16! = 20 922 789 888 000 початкових позицій.
Це з урахуванням розташувань порожній клітини. Наприклад, ось така позиція.
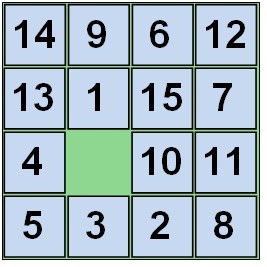
Якщо ж розглянути, що порожня клітка завжди знаходиться на одному місці (наприклад, місце 1 - лівий верхній кут - або місце 16 - правий нижній кут, порожня позиція), то отримаємо
15! = 1 307 674 368 000 позицій.
Наприклад, ось таке початкове розташування
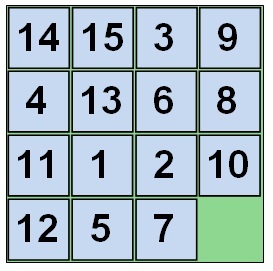
Тут розглядається чітко, що порожня клітка завжди знаходиться в правому нижньому кутку.
Половина з усіх розкладів вирішується. Інша половина не збирається, так як приходить ось до такого стану:
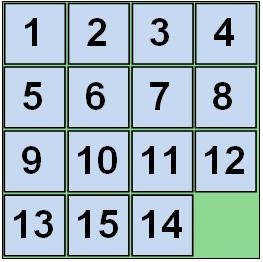
Як пам'ятаємо, це завдання Лойда.
Сподіваюся, ви зрозуміли, що 50% розкладів зібрати не вдасться.
Будь-яку початкову позицію можна перевірити на решаемость. Причому не треба намагатися її зібрати і подивитися на кінцеве розташування 15 і 14. Для цього достатньо лише вирахувати «Парність розкладу», «Параметр безладу» (це поняття хто як хоче, так і називає). В реалі дійсно швидше просто зібрати за півхвилини фішки і подивитися що вийшло, ніж лічити про себе многоціфар. Але для повноти картини вивчимо теорію. Визначення парності досить складне. Давайте подивимося, що пише Вікіпедія:
Можна показати, що рівно половину з усіх можливих 20 922 789 888 000 (= 16!) Початкових положень квача н евозможно привести до зібраного увазі: нехай квадратик з числом i розташований до (якщо вважати зліва направо і зверху вниз) k квадратиків з числами меншими i. Будемо вважати n i = k. тобто якщо після кісточки з i-му числом немає чисел, менших i. то k = 0. Також введемо число e - номер ряду порожній клітини (рахуючи з 1). якщо сума
є непарної, то рішення головоломки не існує
Є ще одне визначення, що попалося на очі:
головоломка має рішення, якщо так званий параметр безладу (число пар чисел, в яких більша кількість передує меншому з додатком номера горизонтального ряду з порожньою кліткою), парний
Хоч воно і простіше, сенс і раніше складно вловити.
Спробуємо пояснити більш простою мовою, як підрахувати Парність.
Для цього потрібно порівнювати пари чисел. Вважаємо кількість тих пар, в яких більша кількість передує меншому. Порівняння ведеться щодо правильного порядку. Тільки в кінці не забуваємо додати номер ряду з порожньою кліткою - це число від 1 (верхній рядок) до 4 (нижня рядок). Візуально можна уявити так:
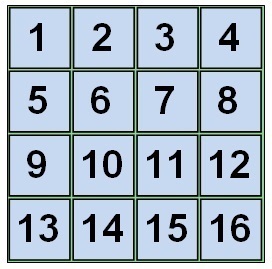
Тут вказані номери позицій. Відповідно, чим менше номер, тим більш рання позиція (сподіваюся, цей момент зрозумілий).
Наприклад, візьмемо ось такий розклад:
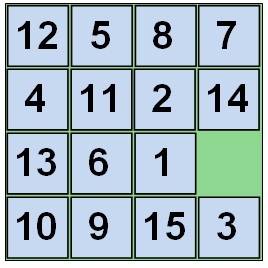
Тут порівнюючи пару 5 і 2 бачимо, що 5. яка стоїть раніше, більше двійки (2). значить це одна потрібна нам для рахунку пара, її ми порахуємо. А 8 менше 11, і варто раніше, значить таку пару не вважаємо.
Трохи теорії: Всього є 15 фішок, що утворює 105 пар (14 + 13 + 12 +. +1). На практиці порівняти 105 пар не так вже й складно, тільки треба їх чітко підраховувати. Наприклад, можна вчинити так (див. Малюнок вище):
Спочатку беремо перше число (у нас 12). Вважаємо, скільки чисел менше знаходиться після нього. На прикладі це одинадцять чисел (від 1 до 11 - ці числа менше і розташовані пізніше, тобто після розглянутого нами числа 12). Результат записали.
Тепер беремо друге число (5). Вважаємо, скільки менших чисел стоїть після нього (не "до", а саме «після» - це для нев'езжающіх). Після п'ятірки тільки чотири числа молодше (від 1 до 4). Результат додали до минулого значенням (11 + 4 = 15).
Тепер беремо третє число (8) і вважаємо також кількість менших чисел, що стоять після (їх шість, тобто від 1 до 7 не рахуючи 5, так як п'ятірка варто раніше).
Так і продовжуємо далі.
Не забуваємо в самому кінці додати ряд з порожньою кліткою. У нас на прикладі це третій ряд.
Ми тут не будемо повністю вважати парність, ці обчислення лише приклад як потрібно робити. Та й нудно це математикою займатися в таких обсягах.
Всього підрахунок займе хвилин 5-10. Якщо отримана сума парна - позиція збереться. Якщо інакше (непарна) - щось не збереться.
Нерозв'язних розклад (нерозв'язних закінчення) Лойда має парність «1» (там тільки 15 передує 14-і і більше нього).
