До пасивних елементів електричних ланцюгів відносяться резистори (R), котушки індуктивності (L) і конденсатори (С). Вони є лінійними елементами, якщо їх опір, індуктивність і ємність залишаються постійним при будь-якій напрузі і струмі.
Частотні характеристики пасивних елементів електричних ланцюгів - це залежність їх опору і фазового зсуву (φ) між напругою і струмом від частоти (f).
Реальні пасивні елементи електричних ланцюгів мають як опором R. так і індуктивністю L. і ємністю C. Однак у багатьох випадках деякими характеристиками елемента можна знехтувати через їх меншовартості в порівнянні з більш значущим. Тобто у резистора можна знехтувати індуктивністю і ємністю, у котушки індуктивності можна знехтувати опором і ємністю, а у конденсатора можна знехтувати опором і індуктивністю. Такі елементи електричних ланцюгів називаються ідеальними, і вони використовуються як для подання реальних елементів, так і для складання схем їх заміщення в розрахункових схемах. Надалі розглянемо ідеальні пасивні елементи електричних ланцюгів.
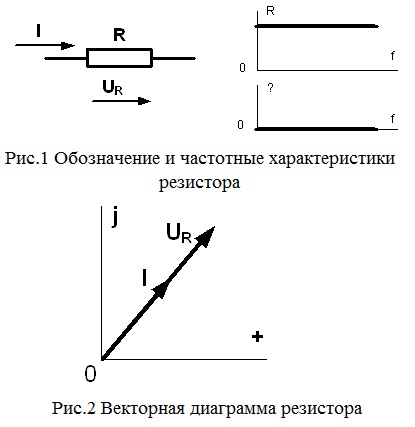
Резистор - це елемент електричного кола, що перетворює електричну енергію в інші види енергії (теплову, механічну, світлову, хімічну). З визначення видно, що резистором на схемі електричного кола можна позначати будь-який елемент, який споживає активну енергію, потужність якої може бути розрахована за формулами:
U- діюче значення прикладеного до резистору напруги (В);
Математична модель резистора
В лінійних електричних ланцюгах прийнято (з певним допущенням), що опір резистора не залежить від частоти R (f) = const. і він не створює зсуву по фазі між напругою і струмом φ R (f) = 0. Тому його частотні характеристики R (f) і φ R (f) мають вигляд (рис.1).
У зв'язку з відсутністю зсуву фаз на змінному струмі вектори напруги і струму резистора на комплексній площині завжди збігаються по фазі (рис.2).
Котушка індуктивності
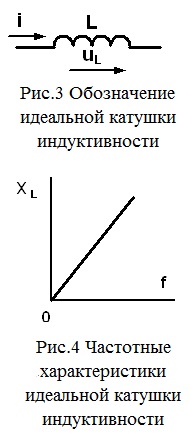
Ідеальна котушка індуктивності - це елемент електричного кола, запасающий електричну енергію в магнітному полі, яку може повністю повернути в подальшому. Тому ідеальна котушка індуктивності активну енергію не споживає, і її активна потужність дорівнює нулю
Математична модель ідеальної котушки індуктивності відображає те, що прикладена до неї напругу uL врівноважується ЕРС самоіндукції e.
де L- індуктивність котушки, яка вимірюється в Генрі (Гн).
На змінному струмі котушка має індуктивний опором
яке може бути визначено через діюче значення напруги на котушці і діюче значення протікає по ній струму за формулою:
У той же час зсув по фазі між напругою і струмом ідеальної котушки індуктивності дорівнює π / 2.
Частотні характеристики ідеальної котушки індуктивності XL (f) представлені на рис.4.
У комплексній формі опір ідеальної котушки індуктивності чисто уявне.
і закон Ома для ідеальної котушки індуктивності в комплексній формі має вигляд
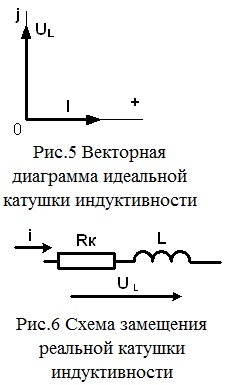
Векторна діаграма, відповідна цій формулі, представлена на рис.5.
З неї видно, що напруга на ідеальній котушці індуктивності випереджає струм наπ / 2.
Однак реальна котушка індуктивності намотана дротом, що володіє активним опором Rk. Тому реальна котушка індуктивності споживає активну енергію, і її активна потужність визначається формулою.
У той же час максимальний запас енергії в магнітному полі котушки індуктивності характеризується її реактивної потужністю Q. вимірюваної в Вар.
конденсатор
Конденсатор - це елемент електричного кола, запасающий електричну енергію в електричному полі, яку може повністю повернути в подальшому. Тому конденсатор активну енергію не споживає, і його активна потужність дорівнює нулю (P = 0).
Математична модель конденсатора
де С - ємність конденсатора, яка вимірюється в Фарадах (Ф) або в мікрофарадах (1 мкФ = 10 -6 Ф).
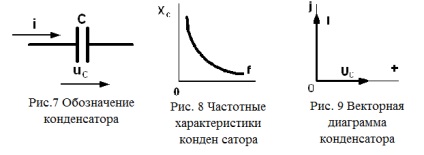
На змінному струмі конденсатор володіє ємнісним опором.
яке може бути визначено через чинне напруга на конденсаторі і протікає через його діючий струм за формулою:
Відповідно до формули опору конденсатора видно, що воно обернено частотеf.
У той же час зсув по фазі між напругою і струмом конденсатора дорівнює -π / 2.
У комплексній формі опір конденсатора чисто уявне.
Закон Ома для конденсатора в комплексній формі має вигляд
Векторна діаграма, відповідна цій формулі, представлена на рис.9.
З неї видно, що струм конденсатора випереджає напругу наπ / 2.
Можливо Вам будуть корисні наступні статті по темі: