Сфера (куля) являє собою єдине геометричне тіло, поверхня якого перетинається площиною будь-якого положення завжди по колу.
Січні площині, що проходять через вертикальну вісь сфери, розсікають її по меридіанах. Січні площині, що проходять перпендикулярно до вертикальної осі сфери, розсікають її по паралелях. Мал. 90
На рис. 91 зображена сфера в трьох ортогональних проекціях, усічена горизонтально-проецирующей площиною. Ця площина розсікає сферу по колу, яка на горизонтальну площину проектується у відрізок, що співпадає з горизонтальним слідом PП1 січної площини. Фронтальна і профільна проекції цієї окружності изобразятся еліпсами, так як площину зрізу розташована похило до площин П1 і П2.
Побудова еліпса (проекції фігури перерізу сфери площиною) починають з побудови характерних точок.
Характерними точками є:
§ кінці великий (С і D) і малої (А і В) осей еліпса;
§ точки, що лежать на фронтальному нарисі сфери - N і M;
§ точки, що лежать на горизонтальному нарисі сфери (А і В);
§ точки, що лежать на профільному нарисі сфери (Е і F).
Мала вісь еліпса: АВ буде лежати на екваторі. Точки А і В з горизонтальної проекції проектують за допомогою ліній проекційної зв'язку на фронтальну (А1 і В1) і профільну (А3 і В3) проекції екватора.
Велика вісь еліпса розташовується перпендикулярно до малої осі. Для її побудови на горизонтальній проекції з точки О1 проводять перпендикуляр до малої осі АВ. Велика вісь на горизонтальну площину проекцій проектується в точку D1 ≡ С1. З цієї точки з горизонтальної проекції на фронтальну і профільну проводять лінії проекційної зв'язку. Велика вісь на цих площинах проекцій паралельна осі OZ і дорівнює діаметру кола, що лежить в площині зрізу. Це відстань (АВ) вимірюють на горизонтальній проекції і переносять на фронтальну і профільну проекції, отримуючи фронтальну проекцію D2 С2 іпрофільную проекцію D3 С3 великий осі.
Потім будуються точки N і M, що лежать на фронтальному нарисі (меридіані) сфери, а також точки Е і F, що лежать на профільному нарисі сфери.
Фронтальні проекції точок N і M - N2; M2 лежать на фронтальній проекції фронтального нарису сфери (на фронтальному меридіані сфери). Профільні проекції точок N і M - N3; M3 лежать на профільній проекції фронтального нарису сфери.
Профільні проекції точок Е і F - Е3 і F3 лежать на профільній проекції профільного нарису сфери (на профільному меридіані сфери).
Потім будуються проміжні точки: 1, 2, 3, 4 за допомогою допоміжних січних площин. Допоміжні паралелі проводять так, щоб окружність - лінія перетину сфери проектувалася на площину проекцій без спотворення. В даному випадку паралелі повинні бути паралельні фронтальній площині проекцій. Проводимо площині: R1 і Q1. розсікають сферу по колу радіусами r1 іr2 .Точкі 1, 2, 3, 4 лежать на цих кіл. Радіус паралелі завжди змиритися в даній площині від осі поверхні обертання до нарису.
Взаємне перетинання поверхонь,
одна з яких - багатогранна
Для закріплення теми «Перетини поверхонь площиною» і наочного уявлення корисності пройденого пропонуємо кілька прикладів.
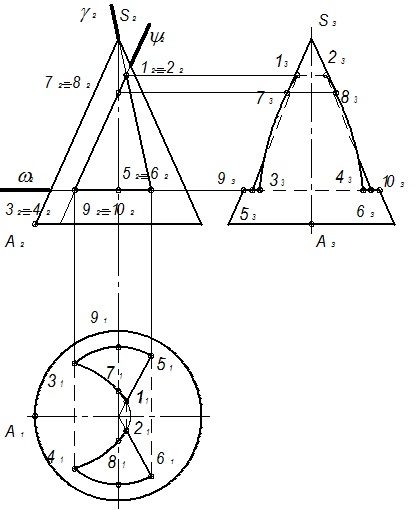
На рис. 95 і 96 наведені побудови наскрізних багатогранних отворів тіл обертання.
Постарайтеся без додаткових пояснень розібратися в побудовах. На кресленнях вказані всі необхідні для побудови характерні точки.
При вирішенні завдань на перетин поверхонь площину слід дотримуватися алгоритму побудови:
1. Визначити в просторі форму лінії перетину поверхні, заданими площинами.
2. Визначити форму проекції лінії перетину на всіх площинах проекцій, на яких за умовами задачі виконуються зображення.
3. на проекції перетину, яка зображується прямою лінією, що збіглася зі слідом січної площини, позначити проекції характерних точок шуканої лінії:
3.1. точки, що належать нарисів поверхонь;
3.2. точки, за якими можна побудувати графічним прийомом всю лінію: для еліпса - велику і малу осі; для параболи і гіперболи - вершини і кінці найбільшої хорди, для багатокутника - його вершини.
4. Побудувати відсутні проекції точок на кресленні.
5. Побудувати проміжні точки лінії перетину і з'єднати всі крапки з урахуванням видимості.
6. Обвести існуючий нарис.
7. Провести прямі захід січних площин з урахуванням видимості.
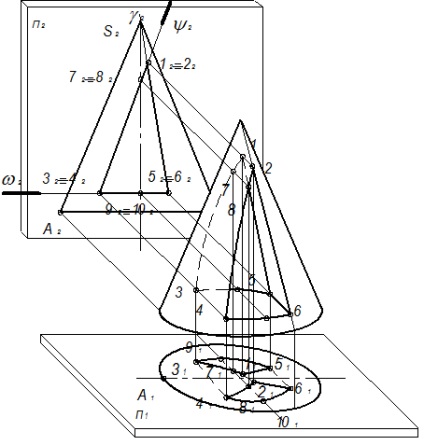
У перетині конуса (рис. 95):
1. площиною # 936; виходить парабола, так як площину паралельна одній що утворює конуса SА;
2. площиною # 969; - коло радіуса О2 Т2;
3. площиною # 966; - трикутник, так як площину проходить через вершину конуса;
4. точки 7 і 8 називаються точками-межами видимості для профільної проекції, так як вони лежать на утворюють конуса, нарисових для профільної проекції конуса.
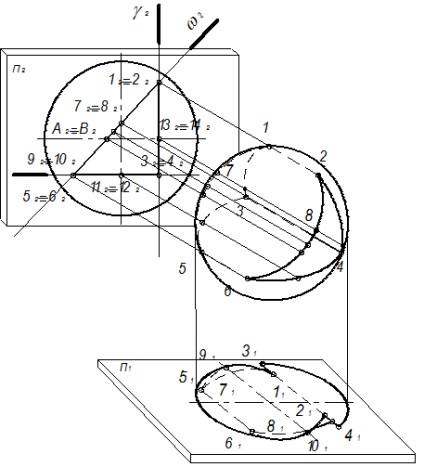
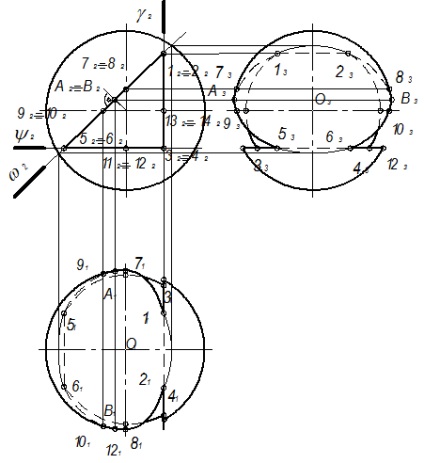
На рис. 96 всі три площини # 947 ;, # 968 ;, # 969; перетинають сферу по колу, але проектуються вони по-різному на різні площини проекцій.
1. Точки 9, 10, 13, 14 - точки-межі видимості для профільної проекції.
2. Точки 7, 8, 11, 12 - точки-межі видимості для горизонтальної проекції.
3. А, В, С, В - кінці осей еліпсів, в які на П1 і П2 проектується коло площині # 969 ;.
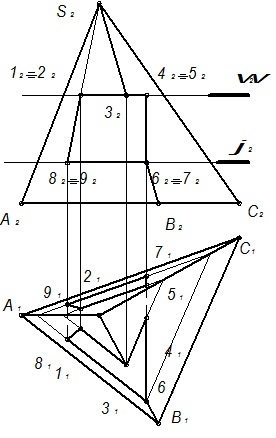
На рис. 97 заданий епюр тригранної піраміди з трапецеїдальним вікном. Розберіться в побудовах. Побудуйте самі профільну проекцію.