Розділ ІІ. стереометрії
2. Перетини призми.
Розглянемо деякі найпростіші перетину призми.
Перетин призми, який проходить через два бічних ребра, які не належать одній основі, називають діагональним перерізом.
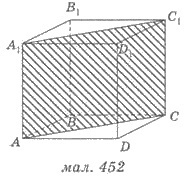
На малюнку 452 АА 1 З 1 З - діагональний переріз прямої призми. Це перетин є прямокутником, одна з його сторін - діагональ підстави АС, а інша - бічне ребро АА 1. У похилій призмі діагональним перерізом є паралелограм.
Часто в задачах необхідно не тільки побудувати переріз, а й знайти його площу або периметр, або використовувати перетин з іншою метою.
Приклад 1. В основі прямої призми лежить ромб зі стороною 4 см і гострим кутом 60 °. Знайти площу діагонального перерізу призми, однією зі сторін якого є велика діагональ ромба, якщо бічне ребро призми дорівнює 2 см.
Рішення. 1) Нехай ABCDA 1 B 1 C 1 D 1 - призма, в основі якої лежить ромб ABCD. АВ = 8 см, A = 60 °, АС - велика діагональ ромба (рис. 452). Тоді АСС 1 А1 - діагональний переріз, площа якого необхідно знайти. CC 1 = 2 см (за умовою).
3) В Δ ADC по теоремі косинусів:
Часто в задачах розглядають перетину призми, що проходять через сторону основи призми і які перетинають бічні ребра призми.
Приклад 2. В основі прямої призми лежить рівносторонній трикутник, сторона якого дорівнює 2 см. Через сторону цього трикутника проведено розтин, яке утворює кут 30 ° з площиною основи і перетинає бічне ребро в його середині. Знайти довжину бічного ребра призми.
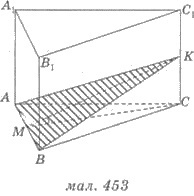
Рішення. 1) Нехай АВСА1 В1 З 1 - трикутна призма, основа якої - трикутник АВС, АВ = 2 см (рис. 453).
2) Через сторону АВ основу трикутника проведено розтин АВК, де К - середина СС 1.
3) Проведемо в трикутнику АВС медіану СМ, яка також є висотою цього трикутника.
4) Оскільки CM AB і CM є проекцією КМ на площину АВС, то по теоремі про три перпендикуляри: КМ АВ.
Тоді КМС - кут, який утворює перетин з площиною основи. За умовою КМС = 30 °.
6) Так як К - середина СС 1. то СС 1 = 2КС = 1 ∙ 2 = 2 (см).