13. Алгоритми пошуку, вибірки і сортування.
Алгоритм послідовного пошуку (АПП) послідовно переглядає по одному елементу списку, починаючи з першого, до тих пір, поки не знайде цільової елемент. Передбачається, що перелік не впорядкований.
Найгірший випадок: цільової елемент стоїть у списку останнім або його зовсім немає в списку.
Середній випадок: пошук завжди завершується успішно, або іноді цільове значення в списку відсутня.
Алгоритм двійкового пошуку (АДП):
Двійковий пошук здійснюється на відсортованому списку. Ідея в тому, що список ділиться навпіл, береться середній ел-т і порівнюється з цільовим ел-том. При порівнянні можливий один із трьох результатів: значення рівні, цільове значення менше елемента списку, або цільове значення більше елемента списку. У першому, і найкращому, випадку пошук завершено. В інших двох випадках ми можемо відкинути половину списку. Коли цільове значення менше середнього елемента, ми знаємо, що якщо воно є в списку, то знаходиться перед цим середнім елементом. Коли ж воно більше середнього елемента, ми знаємо, що якщо воно є в списку, то знаходиться після цього середнього елемента. Цього достатньо, щоб ми могли одним порівнянням відкинути половину списку. При повторенні цієї процедури ми зможемо відкинути половину частині списку.
У найгіршому випадку число проходів одно k = log2 (N +1).
Середній випадок A (N) ≈ log2 (N +1) -1
Іноді нам потрібен ел-т зі списку, що володіє деякими спеціальними св-ми, а не має деяке конкретне значення. Наприклад, в списку співробітників знайти середнього за віком або знайти 5 співробітників з найменшою оплатою праці. У більш загальному випадку нас може цікавити запис з К-им за величиною значенням поля. Один із способів знайти такий запис полягає в тому, щоб впорядкувати список в порядку убування; тоді запис з К-им за величиною значенням виявиться на К-му місці. На це піде набагато більше сил, ніж необхідно: значення, менші шуканого, нас, насправді, не цікавлять. Може стати в нагоді наступний підхід: ми знаходимо найбільше значення в списку і поміщаємо його в кінець списку. Потім ми можемо знайти найбільше значення в частині списку, виключаючи вже знайдене. В результаті ми отримуємо друге за величиною значення списку, яке можна помістити на друге з кінця місце в списку. Повторивши цю процедуру До раз, ми знайдемо К-е за величиною значення.
На кожному кроці алгоритму ми вибираємо один з елементів вхідних даних і вставляємо його на потрібну позицію в уже відсортованому списку, до тих пір, поки набір вхідних даних не буде вичерпаний. Метод вибору чергового елементу з початкового масиву довільний; може використовуватися практично будь-який алгоритм вибору. Зазвичай (і з метою отримання стійкого алгоритму сортування), елементи вставляються по порядку їх появи у вхідному масиві. Наведений нижче алгоритм використовує саме цю стратегію вибору.
Вхід: масив A, що складається з елементів A [1], A [2]. A [n]
while j> 0 and A [j]> key:
Час виконання алгоритму залежить від вхідних даних: чим більша безліч потрібно впорядкувати, тим більший час виконується сортування. Також на час виконання впливає вихідна впорядкованість масиву. Так, кращим випадком є відсортований масив, а гіршим - масив, відсортований в порядку, зворотному потрібного. Тимчасова складність алгоритму при гіршому варіанті вхідних даних - θ (n²).
Алгоритм складається в повторюваних проходах по сортованого масиву. За кожен прохід елементи послідовно порівнюються попарно і, якщо порядок в парі невірний, виконується обмін елементів. Проходи по масиву повторюються до тих пір, поки на черговому проході не опиниться, що обміни більше не потрібні, що означає - масив відсортований. При проході алгоритму, елемент, що стоїть нема на своєму місці, «спливає» до потрібної позиції як бульбашка у воді, звідси і назва алгоритму.
При сортуванні Шелла спочатку порівнюються і сортуються між собою значення, віддалені один від одного на деякій відстані d. Після цього процедура повторюється для деяких менших значень d, а завершується сортування Шелла упорядкуванням елементів при d = 1 (тобто, звичайної сортуванням вставками). Ефективність сортування Шелла в певних випадках забезпечується тим, що елементи «швидше» встають на свої місця.
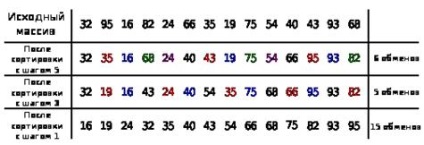
Приклад. Нехай дано список A = (32,95,16,82,24,66,35,19,75,54,40,43,93,68) і виконується його сортування методом Шелла, а в якості значень d обрані 5,3 , 1.
На першому кроці упорядковано підсписки A, складені з усіх елементів A, різняться на 5 позицій, тобто підсписки A5,1 = (32,66,40), A5,2 = (95,35,43), A5,3 = ( 16,19,93), A5,4 = (82,75,68), A5,5 = (24,54).
В отриманому списку на другому кроці знову упорядковано підсписки з віддалених на 3 позиції елементів.
Процес завершується звичайної сортуванням вставками отриманого списку.
Загальний список розбивається на стопки відповідно до розряду ключа. При кожному проході здійснюються перестановки у відповідності зі значенням окремої частини ключа. Після кожного проходу відбувається об'єднання стопок і їх розбиття по іншому розряду ключа.
Рекурсивний алгоритм сортування. Вибравши елемент в списку, швидке сортування ділить з його допомогою список на дві частини. В одній частині елементи більше обраного, в іншій - менше.
Алгоритм сортування, який впорядковує списки (або інші структури даних, доступ до елементів яких можна отримувати тільки послідовно, наприклад - потоки) в певному порядку.
- Сортований масив розбивається на дві частини приблизно однакового розміру;
- Кожна з вийшов частин сортується окремо, наприклад - тим же самим алгоритмом;
- Два упорядкованих масиву половинного розміру з'єднуються в один.
Рекурсивне розбиття завдання на менші відбувається до тих пір, поки розмір масиву не досягне одиниці (будь-який масив довжини 1 можна вважати впорядкованим).