Числа i і j утворюють в перестановці інверсію. якщо i> j, але i розташоване раніше j. Якщо число інверсій в перестановці парне, то перестановка називається парної. в іншому випадку непарної. Наприклад, перестановка (4 7 1 5 3 6 2) парна, так як число інверсій в ній 12 парне. Для визначення числа інверсій в перестановці слід вибрати порядок їх підрахунку. Найпростіше підраховувати скільки інверсій утворює число з подальшими числами перестановки:
Inv (4 7 1 5 3 6 2) = 3 + 5 + 0 + 2 + 1+ 1+ 0 = 12.
Операція транспозиції полягає в зміні місцями двох елементів перестановки.
Теорема. Одна транспозиція змінює парність перестановки на протилежну.
Доведення. Теорема очевидна, якщо операції транспозиція піддані два сусідніх числа перестановки. Нехай тепер між числами i і j знаходиться s чисел. Для того, щоб число j виявилося на місці i, його слід поміняти місцями з сусідніми s + 1 раз. А щоб потім число i зайняло місце числа j його слід поміняти місцями з сусідніми s раз. Всього необхідно провести операцію транспозиція над сусідніми числами s + 1 + s = 2s + 1нечетное число раз. Отже, парність перестановки зміниться на протилежну. # 9632;
Взаємно однозначне відображення безлічі з n елементів на себе називається підстановкою n- го ступеня. Підстановки прийнято записувати в наступному вигляді
Тут ми працюємо, як це часто робиться в комбінаториці, не з самими елементами будь-якого безлічі, а з їх номерами. У верхньому рядку-чисельнику розташовані елементи множини, а в нижній сходинці-знаменнику розташовані ті елементи, в які переходять відповідні елементи чисельника при відображенні f, тобто. Звичайно, елементи чисельника можуть бути розташовані в іншому порядку, ніж природний. Тут підстановка записана в канонічному вигляді, коли порядок номерів в чисельнику природний. І в чисельнику і в знаменнику підстановки стоять перестановки n-го ступеня. Якщо сума інверсій в чисельнику і знаменнику парна, то підстановка називається парної. в іншому випадку непарної. При будь-заміні місцями стовпців підстановки її парність не змінюється. Для канонічної записи підстановки
Безліч всіх підстановок n- го ступеня позначається через. Число всіх підстановок n -йстепені одно n!. Введемо на множині S операцію множення - композицію відображень. Приклад множення підстановок:
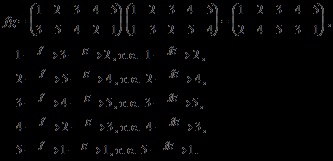
Теорема. Безліч всіх підстановок n- го ступеня утворює групу щодо операції композиції відображень.
Для доказу необхідно перевірити виконання всіх аксіом групи. # 9632;
Нейтральним елементом є тотожне відображення
Зворотним елементом для підстановки є підстановка