План-графік розміщення замовлень на поставки товарів, виконання робіт, надання послуг для потреб

УРОК: «РОЗКЛАДАННЯ ВЕКТОРА ПО ДВОХ неколінеарна вектор»

Тема: Розкладання вектора по двом неколінеарна векторах

Клас: 9 клас
Педагог :. заступник директора з виховної роботи. учитель математики та інформатики.

Установа освіти: МОУ Шуринську середня загальноосвітня школа Кемеровської області
Місто: Кемеровська область

Знати формулювання і доказ леми про колінеарних векторах і теорему про розкладання по двом неколінеарна векторах;

Вміти вирішувати задачі, застосовуючи отримані знання.

I.Організаціонний момент: назвати цілі уроку.

III.Об'ясненіе нового матеріалу:

1. Розпад вектора по двом неколінеарна векторах.

При вирішенні завдань часто виникає необхідність висловити будь-якої вектор через вже задані вектори. Така операція називається розкладанням вектора по неколінеарна векторах.

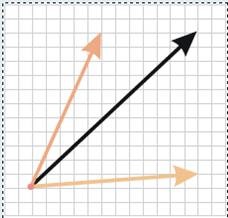
2. Лемма про колінеарних векторах.

Лемма - це допоміжне твердження, за допомогою якого доводиться наступна теорема або декілька теорем.

Теорема: Якщо вектори і колінеарні і # 61 625; 0, то існує таке число k, що = k.

Так що розглядаються вектори, за умовою колінеарні, то вони можуть мати однакові напрямки. Розглянемо два випадки, коли вектори і сонаправлени і протилежно спрямовані.

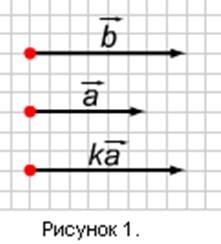
1). Візьмемо число. Так як k ³0, то вектори k і сонаправлени (рисунок 1). Крім того, їх довжини рівні: ½k ½ = ½ k½½ ½ = ½ ½ = ½ ½. Тому = k

2). Візьмемо число. Так як k<0, то векторы k и снова сонаправлены (рисунок2). Их длины также равны: ½k½=½ k½½½ = ½½=½½. Поэтому = k

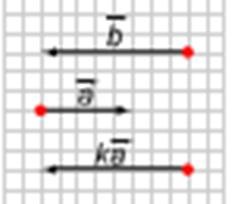
3. Теорема про розкладання вектора по двом неколінеарна векторах.

Теорема: Будь-який вектор можна розкласти по двом даними неколінеарна векторах, причому коефіцієнти розкладання визначаються єдиним чином.

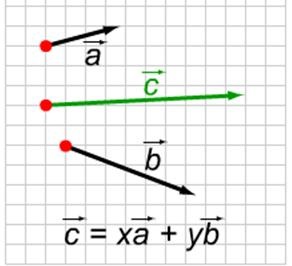
Нехай і - дані неколінеарна вектори, вектор представлений у вигляді

= Х + у, де х і у - деякі числа. Прийнято говорити, що вектор розкладений по векторах і. Числа х і у називаються коефіцієнтами розкладання.

Можливі два випадки:

1) Вектор коллінеарен одному з векторів і, наприклад, вектору (рісунок1). В цьому випадку по лемі про неколінеарних векторах вектор можна представити у вигляді = у, де у - деяке число, і, отже, = 0 + у, т. Е. Вектор розкладанні по векторах

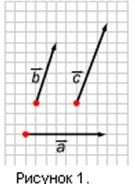
2) Вектор НЕ коллінеарен ні вектору, ні вектору. Відзначимо якусь точку О і відкладемо від неї вектори =, =, = (Рисунок2).

Через точку Р проведемо пряму, паралельну прямій ОВ, і позначимо через А1 точку перетину цієї прямої з прямою ОА. За правилом трикутника = +. Але вектори і колінеарні відповідно векторах і, тому існує числа х і у, такі, що = х, = у. Отже, = х + у, т. Е. Вектор розкладений по векторах і.

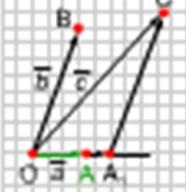
Доведемо тепер, що коефіцієнти х і у розкладання визначаються єдиним чином. Припустимо, що поряд з розкладанням = х + у має місце інше розкладання = х1 + в1. Віднімаючи друга рівність з першого і використовуючи правила дій над векторами, отримуємо = (х-х1) + (у-у1). Це рівність може виконуватися тільки в тому випадку, коли коефіцієнти х-х1 і у-у1 дорівнюють нулю. Справді, якщо припустити, наприклад, що х-х1 ¹0, то з отриманого рівності знайдемо = -, а значить вектори і колінеарні. Але це суперечить умові теореми. Отже, х-х1 = 0 иу-у1 = 0, звідки х = х1 і у = у1. Це і означає, що коефіцієнти вектора визначаються єдиним чином. Теорема доведена.

1.Лемма - це допоміжне твердження, що вживається при доказі однієї або декількох теорем.

2. Лемма (про колінеарних векторах). Якщо вектори і колінеарні і вектор ¹0, то існує таке число k, при якому = k

3. Нехай і - дані неколінеарна вектори, вектор представлений у вигляді

= Х + у, де х і у - деякі числа. Прийнято говорити, що вектор розкладений по векторах і. Числа х і у називаються коефіцієнтами розкладання.

4. Теорема: Будь-який вектор можна розкласти по двом даними неколінеарна векторах, причому коефіцієнти розкладання визначаються єдиним чином.

IV. Закріплення отриманих знань:

1.Діагоналі паралелограма АВСDпересекаются в точці О. Виразіть векторчерез векториі.

3.№ 000 (б) .Найдіте таке чіслоk, щоб виконувалося рівність = k, якщо відомо, що векториісонаправлени і½½ = 12 см, ½½ = 24 дм.

4.№ 000 (а, г). Діагоналі паралелограма перетинаються в точці О, М - середина відрізка АТ. Знайдіть, якщо це можливо, таке число k, щоб виконувалося рівність: = k, = k

5. Дан довільний трикутник АВС з медіаною АD. Знайдіть, як вектор виражається через вектори і.

V. Підведення підсумків.

VI. Завдання додому: п. 86, №№ 000 (в, г), 912 2,3 стовпчик), 916 (в, г)