Мета: набуття навичок знаходження натуральної величини перетину прямої призми методом заміни площин.
Контрольні питання:
1. Який вид має перетин многогранника.
2. У якому випадку проекція перетину прямої призми визначається за кресленням без додаткових побудов?
Завдання 1: методом заміни площин проекцій знайти натуральну величину перерізу прямої призми фронтально-проектує площиною; об'єкти задані проекціями на горизонтальну і фронтальну площину (варіанти завдань наведені в додатку В).
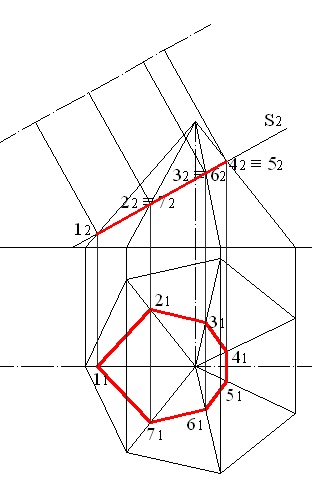
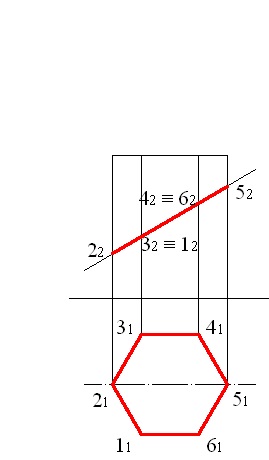
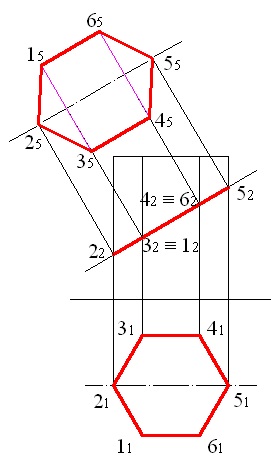
Вирішимо задачу за допомогою одноразової заміни площин проекцій. Фігура перерізу являє собою шестикутник, який зображається на фронтальній площині проекцій відрізком прямої, а на горизонтальній площині проекцій як багатокутник, що співпадає з горизонтальною проекцією призми (рис. 5.1).
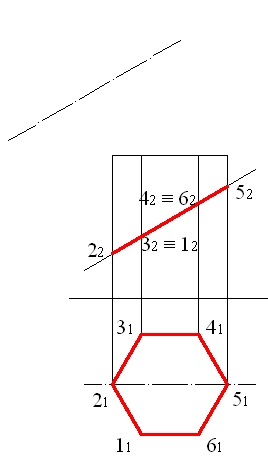
Спроектуємо вісь симетрії на додаткову площину, для цього
за допомогою команди OFFSET, проводимо штрих-пунктиром, паралельну фронтальному сліду січної площини (рис. 5.2). Відстань між паралельними лініями може бути будь-яким, рекомендується вибрати його так, щоб результат побудови не накладається на фронтальну проекцію призми.
Малюнок 5.1 - Проекції перетину прямої шестигранної призми
Малюнок 5.2 - Проектування осі симетрії на додаткову площину
Тепер можна знайти проекції точок 1 - 6 на додаткову площину:
побудуємо перпендикуляри з точок 22. 32. 42 і 52 (рис. 5.3) на вісь симетрії, при цьому будуть отримані проекції точок 2 і 5;
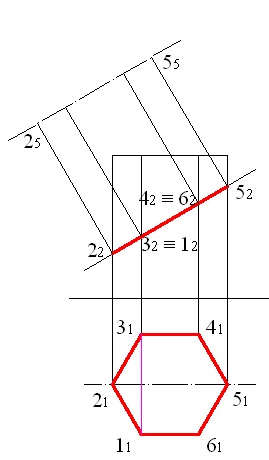
щоб побудувати проекції точок 1, 3, 4 і 6, знайдемо відстань між точками 1 і 3, для цього з'єднаємо горизонтальні проекції цих точок відрізком (рис. 5.4), довжина відрізка буде дорівнює відстані між точками, тому що він паралельний горизонтальній площині;
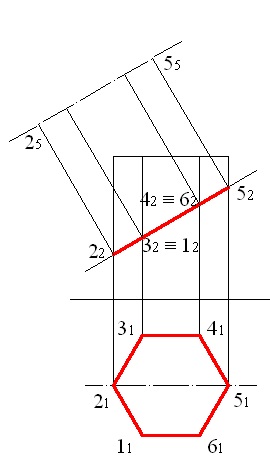
Малюнок 5.3 - Проектування точок 2 і 5
Малюнок 5.4 - Відшукування відстані між точками 1 і 3
за допомогою команди ALIGN побудуємо проекцію отриманого відрізка на площину П5. таким чином, будуть знайдені точки 15 і 35 (рис. 5.5);
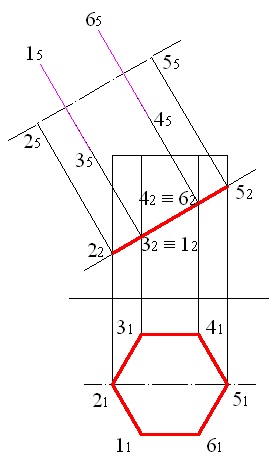
враховуючи, що відстань між точками 4 і 6 в даному випадку збігається з відстанню між точками 1 і 3, скопіюємо отриманий відрізок і отримаємо точки 45 і 65 (рис. 5.6).
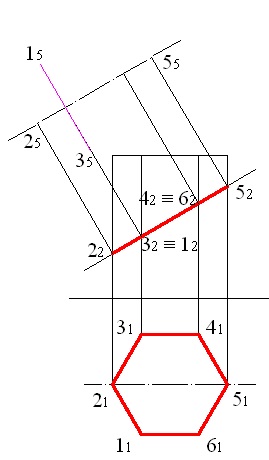
Малюнок 5.5 - Побудова проекцій точок 1 і 3
Малюнок 5.6 - Побудова проекцій точок 4 і 6
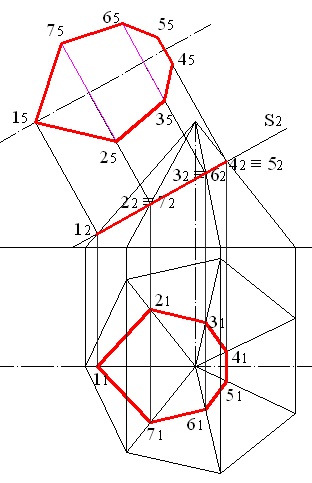
Так як площину П5 паралельна січній площині, точки 15. 25. 35. 45. 55 і 65 є вершинами шестикутника, що представляє собою натуральну величину перерізу (рис. 5.7).
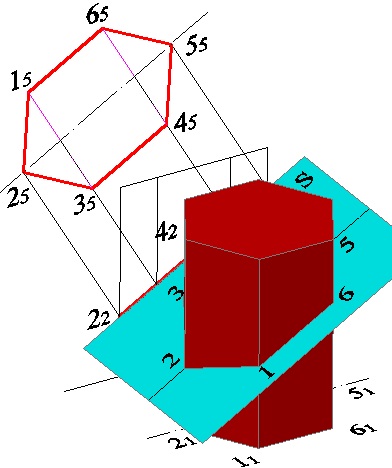
На малюнку 5.8 приведена тривимірна модель розглянутого побудови.
На малюнку 5.9 показаний випадок, коли січна площина проходить через верхню основу призми.
У разі, якщо підстава призми не має осі симетрії, слід провести лінію з крайньої зліва чи справа вершини, потім вимірювати і відкладати на площину П5 відстані до неї (рис 5.10).
Малюнок 5.10 - Відсутність осі симетрії
Завдання 2: методом заміни площин проекцій знайти натуральну величину перерізу піраміди фронтально-проектує площиною; (Варіанти завдань наведені в додатку В).
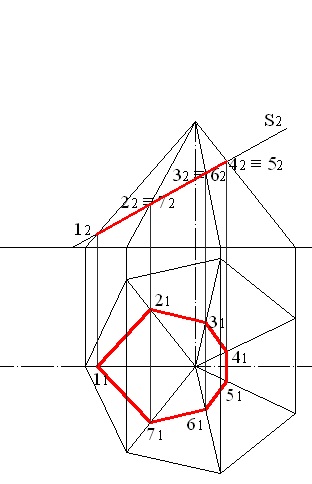
Розглянемо відшукання натуральної величини перетину семикутною піраміди фронтально-проектує площиною. Вихідний креслення наведено на рис. 5.11. На відміну від розглянутого вище випадку, горизонтальна проекція перетину не збігається з проекцією підстави. Її необхідно знайти, використовуючи фронтальні проекції точок перетину ребер з січною площиною, горизонтальні проекції цих точок визначаємо за співвідношенням (рис. 5.12). Перетин є семикутник, вершини його - точки 1, 2, 3, 4, 5, 6, 7.
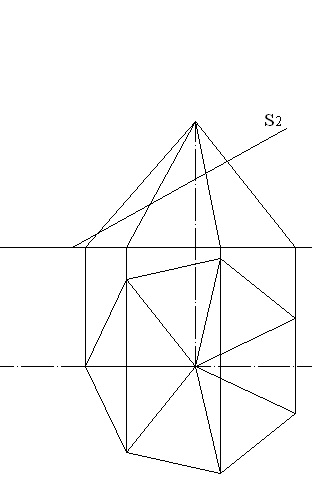
Малюнок 5.11 - Піраміда і січна площина
Малюнок 5.12 - Горизонтальна проекція перетину піраміди
Для відшукання натуральної величини перетину побудуємо проекцію осьової лінії на площину, паралельну перетину. Опустимо на неї перпендикуляри з фронтальних проекцій точок перетину ребер з січною площиною (рис. 5.13). Побудуємо відрізки, що визначають відстань між точками 2 і 7, 3 і 6, 4 і 5. Ці відрізки паралельні горизонтальній площині, тому побудуємо їх між горизонтальними проекціями вищезазначених точок. Спроектуємо отримані відрізки на площину П5. семикутник, який визначається точками 15. 25. 35. 45. 55. 65 і 75 являє собою натуральну величину перерізу (рис. 5.14).