Побудова поверхонь в Mathcad.
Побудова графіка поверхні в системі Mathcad може здійснюватися кількома способами.
1 Побудова поверхонь по матриці аплікат їх точок.
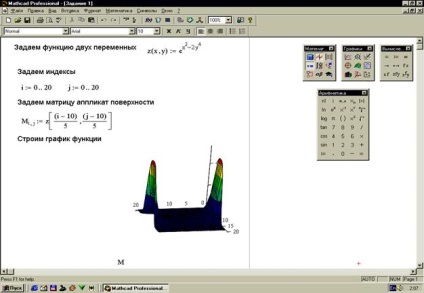
Оскільки елементи матриці М - індексовані змінні з цілочисельними ін-Декс, то перед створенням матриці потрібно задати індекси у вигляді ранжируваних пе-ремінних з цілочисельними значеннями, а потім з них сформувати сітку значень х і у - координат для аплікат z (x, y) . Значення х і у можуть бути будь-якими дійсними числами.
Після зазначених вище визначень вводиться шаблон графіка (або за допомогою підменю меню Вставка, або за допомогою панелі Graph). Лівий верхній кут шаблону поміщається в місце розташування курсора. Шаблон містить єдине місце введення - темний прямокутник у лівого нижнього кута основного шаблону. У нього треба занести ім'я мат-Ріци аплікат поверхні. Після цього треба встановити покажчик миші в стороні від графічного блоку і клацнути лівою кнопкою.
Слід зауважити, так як графік будується на основі матриці, що містить тільки координати висот фігури, то справжні масштаби по осях абсцис і ординат невідомі і на малюнках проставляються. Однак можна виводити порядкові номери елементів матриць в заданому напрямку. Необхідно стежити за тим, як сформувати вектори Х і У. щоб поверхня виглядала природно і була видна необхідної частини поверхні.
2 Побудова тривимірних графіків без завдання матриці.
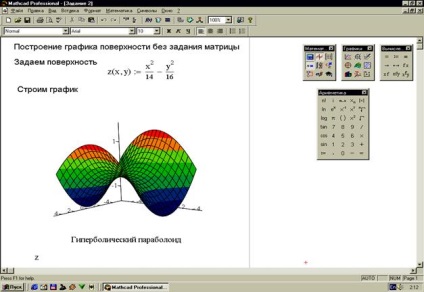
В даному випадку для побудови досить задати функцію змінних х і у. В результаті побудова графіків поверхонь виконується також просто, як і побудова двомірних графіків. Недостат-ками такого побудови є невизначеність в масштабуванні і те, що не всі поверхні другого порядку можна побудувати таким чином.
Форматування тривимірних графіків.
Принцип форматування тривимірних графіків такий же, як і форматування двомірних графіків. Відмінність полягає лише в більшій кількості параметрів форматування.
Завдання 1. Побудувати поверхню по матриці аплікат її точок (рисунок 30).
Завдання 2. Побудувати поверхню без завдання матриці (рисунок 31).
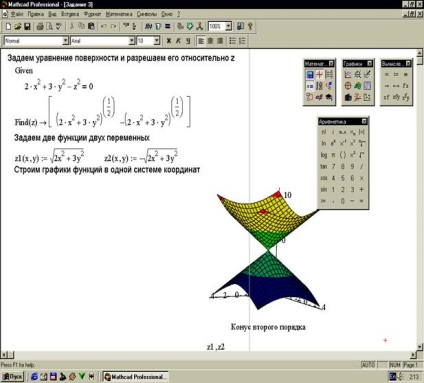
Рівняння поверхні не завжди задається в явному вигляді. Для того щоб побудувати поверхню задану неявно необхідно спочатку рівняння даної поверхні дозволити щодо будь-якої змінної, а потім будувати поверхні за отриманими рівняннями.
Завдання 3. Побудувати поверхню, задану рівнянням (рисунок 32).
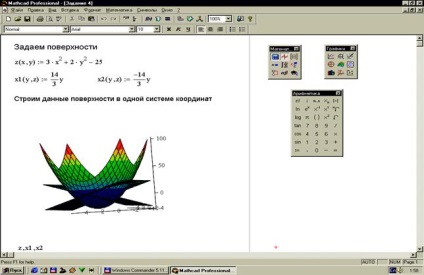
Завдання 4. Побудувати поверхню, задану рівнянням (рисунок 33).
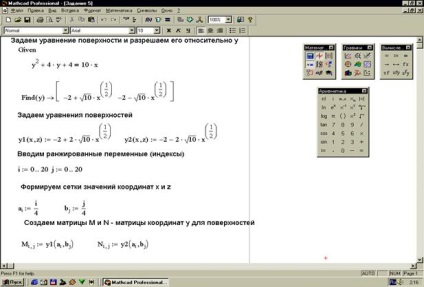
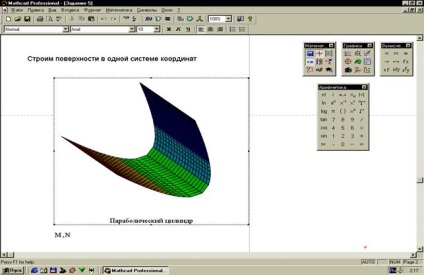
Можливості системи Mathcad дозволяють будувати пересічні поверхні в одній системі координат.
Завдання 5. Побудувати поверхні. (Рисунок 34).
У пакеті Mathcad також можлива побудова поверхонь, заданих в параметричній формі. Приклади таких побудов наведені на малюнках 36 і 37.