Побудова слідів площини - Лекція, розділ Філософія, І. С. Козлова, Ю. В. Щербакова Нарисна геометрія. Конспект лекцій Лекція № 1. Відомості про проекціях Розглянемо Побудова Слідів Площини Р, Яка Задана Парою Перетнув.
Розглянемо побудову слідів площини Р. яка задана парою пересічних прямих I і II (рис. 45).
Якщо пряма знаходиться на площині Р, то її сліди лежать на однойменних слідах площині. Тому сліди площини, які необхідно знайти, повинні проходити через однойменні сліди всіх прямих, що знаходяться в цій площині, т. Е. Знаходимо сліди обох прямих I і II. Поєднавши їх горизонтальні сліди h1 і h2. можна отримати горизонтальний слід Ph площині Р. а якщо з'єднати фронтальні v1. і v2. можна отримати фронтальний слід Pv.
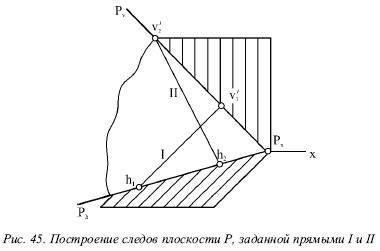
Обидва сліду Ph і Р повинні перетинатися на осі х в точці сходу Рх або виявитися одночасно їй паралельними. Таким способом здійснюється перевірка правильності побудови, т. Е. Для побудови слідів площини можливо обмежитися перебуванням будь-яких трьох слідів двох прямих, що визначають площину.
Всі теми даного розділу:
поняття проекцій
Нарисної геометрії називають науку, яка є теоретичним фундаментом креслення. У даній науці вивчаються способи зображення на площині різних тіл і їх елементо
паралельна проекція
Паралельна проекція - це такий вид проекції, при побудові якого використовуються паралельні проектуються промені. При побудові паралельних проекцій потрібно задати на
Проекції точки на дві площини проекцій
Розглянемо проекції точок на дві площини, для чого візьмемо дві перпендикулярні площині (рис. 4), які будемо називати горизонтальній фронтальної і площинами. Лінію перетину даних плоск
Відсутність осі проекцій
Для пояснення отримання на моделі проекцій точки на перпендикулярні площини проекцій (рис. 4) необхідно взяти шматок цупкого паперу у формі подовженого прямокутника. Його потрібно зігнути між ін
Проекції точки на три площини проекцій
Розглянемо профільну площину проекцій. Проекції на дві перпендикулярні площині зазвичай визначають положення фігури і дають можливість дізнатися її справжні розміри і форму. Але бувають випадки, ко
координати точки
Положення точки в просторі може бути визначено за допомогою трьох чисел, які називаються її координатами. Кожній координаті відповідає відстань точки від якої-небудь площині ін
проекції прямої
Для визначення прямої необхідні дві точки. Крапку визначають дві проекції на горизонтальну і фронтальну площині, т. Е. Пряма визначається за допомогою проекцій двох своїх точок на горизонтальній
сліди прямої
Слід прямий - це точка перетину її з деякою площиною або поверхнею (рис. 20). Горизонтальним слідом прямої називається деяка точка H
Різні положення прямої
Пряму називають прямою загального положення, якщо вона не паралельна і не перпендикулярна ні однієї площини проекцій. Проекції прямої загального положення теж не паралельні і не перпенд
Взаємне розташування двох прямих
Можливі три випадки розташування прямих у просторі: 1) прямі присікаються, т. Е. Мають спільну точку; 2) прямі паралельні, т. Е. Не мають спільної точки, але лежать в одній плоскос
перпендикулярні прямі
Розглянемо теорему: якщо одна сторона прямого кута паралельна площині проекцій (або лежить в ній), то прямий кут проектується на цю площину без спотворення. Наведемо доказ для
Визначення положення площини
Для довільно розташованої площині проекції її точок заповнюють всі три площини проекцій. Тому не має сенсу говорити про проекції всій площині цілком, потрібно розглядати лише проекції
сліди площини
Слід площині Р - це лінія перетину її з даної площиною або поверхнею (рис. 36). Лінію перетину площини Р з горизонтальною площиною називаю
Горизонталі і фронталі площині
Серед прямих, які лежать в деякій площині, можна виділити два класи прямих, що грають велику роль при вирішенні різноманітних задач. Це прямі, які називають горизонталями
Різні положення площини
Площиною загального положення називається площина, що не паралельна і не перпендикулярна ні однієї площини проекцій. Сліди такій площині також не паралельні і не перпендикулярні
Взаємне розташування двох площин
Для двох площин можливі наступні варіанти взаємного розташування: вони паралельні або перетинаються по прямій лінії. З стереометрії відомо, що дві площини паралельні, якщо дві
Пряма, паралельна площині
Може бути кілька положень прямої щодо деякої площини. 1. Пряма лежить в деякій площині. 2. Пряма паралельна деякій площині. 3. Пряма Перес
Пряма, яка перетинає площину
Для знаходження точки перетину прямої і площини необхідно побудувати лінії перетину двох площин. Розглянемо пряму I і площина Р (рис. 54).
Призма і піраміда
Розглянемо пряму призму, яка стоїть на горизонтальній площині (рис. 56). Її бічні гран
Циліндр і конус
Циліндр - це фігура, поверхня якого виходить обертанням прямої m навколо осі i, розташованої в одній площині з цієї прямої. У разі, коли пряма m
Куля, тор і кільце
Коли деяка вісь обертання I є діаметром кола, то виходить кульова поверхню (рис. 66).
Лінії, що застосовуються в кресленні
У кресленні застосовують три основних типи ліній (суцільні, штрихові і штрихпунктирні) різної товщини (рис. 76).
Розташування видів (проекцій)
У кресленні застосовуються шість видів, які зображені на малюнку 85. На малюнку показані проекції літери «Л».
Відступ від наведених правил розташування видів
У деяких випадках можливі деякі правил побудови проекцій. Серед цих випадків можна виділити наступні: часткові види і види, розташовані без проекційної зв'язку з іншими видами.
Число проекцій, що визначають дане тіло
Положення тіл у просторі, форма і розміри визначаються зазвичай невеликим числом відповідним чином підібраних точок. Якщо при зображенні проекції якогось тіла звертати увагу
Обертання точки близько осі, перпендикулярної площини проекцій
На малюнку 91 дана вісь обертання I, яка перпендикулярна горизонтальній площині, і довільно розташована в просторі точка А. При обертанні біля осі I ця точка описание
Визначення натуральної величини відрізка шляхом обертання
Відрізок, паралельний який-небудь площині проекцій, проектується на неї без спотворення. Якщо повернути відрізок таким чином, щоб він став паралельним одній з площин проекцій, то можна опр
Побудова проекцій фігури перерізу можна виконати двояко.
1. Можна знайти точки зустрічі ребер багатогранника з січною площиною, після чого з'єднати проекції знайдених точок. В результаті цього вийдуть проекції шуканого багатокутника. У цьому випадку це
піраміда
На малюнку 98 показано перетин поверхні піраміди фронтально-проектує площиною Р. На малюнку 98б зображена фронтальна проекція а точки зустрічі ребра KS з площиною
косі перетину
Під косими перетинами розуміють коло завдань на побудову натуральних видів перетинів розглянутого тіла проектується площиною. Для виконання косого перетину необхідно розчленувати
Гіпербола як перетин поверхні конуса фронтальною площиною
Нехай потрібно побудувати перетин поверхні конуса, що стоїть на горизонтальній площині, площиною Р, яка паралельна площині V. На малюнку 103 показано фронтальна
Перетин поверхні циліндра
Бувають такі випадки перетину поверхні прямого кругового циліндра площиною: 1) окружність, якщо січна площина Р перпендикулярна осі циліндра, причому вона паралельна основ
Перетин поверхні конуса
У загальному випадку кругова конічна поверхня включає в себе дві абсолютно однакові порожнини, які мають загальну вершину (рис. 107В). Утворюють однієї порожнини представляють собою продовження про
Перетин поверхні кулі
Будь-яке перетин поверхні кулі площиною є колом, яка проектується без спотворення тільки в тому випадку, якщо січна площина паралельна площині проекцій. У загальному ж випадку ми б
косі перетину
Нехай потрібно побудувати натуральний вигляд перерізу фронтально-проектує площиною тіла. На малюнку 110а розглядається тіло, обмежене трьома циліндричними поверхнями (1, 3 і 6), поверхн
піраміда
Щоб знайти сліди прямої на поверхні деякого геометричного тіла, потрібно провести через пряму допоміжну площину, потім знайти перетин поверхні тіла цією площиною. шуканими будуть
Циліндрична гвинтова лінія
Освіта гвинтовий лінії. Розглянемо малюнок 113а на ньому точка М рухається рівномірно по деякій окружності, яка представляє собою перетин круглого циліндра площиною Р. Тут ця плоскос
Два тіла обертання
Метод проведення допоміжних площин застосовується при побудові лінії перетину поверхонь двох тіл обертання. Суть цього методу полягає в наступному. Проводять допоміжну площину
перетину
Існують деякі визначення і правила, які відносяться до перетинів. Перетин - це плоска фігура, яка була отримана в результаті перетину даного тіла некотор
розрізи
Визначення та правила, які відносяться до розрізів. Розріз - це таке умовне зображення предмета, коли його частина, що знаходиться між оком спостерігача і січною пло
Частковий розріз або вирив
Розріз називається повним, якщо зображуваний предмет розтинають цілком, інші розрізи називаються частковими, або вириваючи. На малюнку 120 на вигляді зліва і на плані зроблені повні розрізи. приче