Логічна функція - це функція, в якій змінні приймають тільки два значення: логічна одиниця або логічний нуль. Істинність або хибність складних суджень являє собою функцію істинність або хибність простих. Цю функцію називають булевої функцією суджень f (a, b).
Будь-яка логічна функція може бути задана за допомогою таблиці істинності, в лівій частині якої записується набір аргументів, а в правій частині - відповідні значення логічної функції. При побудові таблиці істинності необхідно враховувати порядок виконання логічних операцій.
Порядок виконання логічних операцій в складному логічному вираженні:
Для зміни зазначеного порядку виконання операцій використовуються дужки.
Для кожного складового висловлювання (логічного виразу) можна побудувати таблицю істинності. яка визначає його істинність або хибність при всіх можливих комбінаціях вихідних значень простих висловлювань (логічних змінних).
При побудові таблиці істинності доцільно керуватися певною послідовністю дій.
Алгоритм побудови таблиць істинності для складних виразів:
1. Визначити кількість рядків:
кількість рядків = 2 n + рядок для заголовка,
n - кількість простих висловлювань.
2. Визначити кількість стовпців:
кількість стовпців = кількість змінних + кількість логічних операцій;
o визначити кількість змінних (простих виразів);
o визначити кількість логічних операцій і послідовність їх виконання.
3. Заповнити стовпці результатами виконання логічних операцій у зазначеній послідовності з урахуванням таблиць істинності основних логічних операцій.
Приклад: Скласти таблицю істинності логічного виразу:
1. Визначити кількість рядків:
на вході три простих висловлювання: А, В, С тому n = 3 і кількість рядків = 2 3 +1 = 9.
2. Визначити кількість стовпців:
o прості вирази (змінні): А, В, С;
o проміжні результати (логічні операції):
o а також шукане остаточне значення арифметичного виразу:
3. Заповнити стовпці з урахуванням таблиць істинності логічних операцій.
Скласти логічну функцію для заданої таблиці істинності.
Правила побудови логічної функції по її таблиці істинності:
1. Виділити в таблиці істинності ті рядки, в яких значення функції дорівнює 1.
2. Виписати шукану формулу у вигляді диз'юнкції декількох логічних елементів. Число цих елементів дорівнює числу виділених рядків.
3. Кожен логічний елемент в цій диз'юнкції записати у вигляді кон'юнкції аргументів функції.
4. Якщо значення будь-якого аргументу функції у відповідному рядку таблиці равно0. то цей аргумент взяти з запереченням.
1. У першій і третій рядках таблиці істинності значення функції дорівнює 1.
2. Так як рядки дві, отримуємо диз'юнкцію двох елементів: () V ().
3. Кожен логічний елемент в цій диз'юнкції Запишіть у вигляді кон'юнкції аргументів функції X і Y. (X Y) V (X Y).
4. Беремо аргумент з запереченням якщо його значення у відповідному рядку таблиці дорівнює 0 і отримуємо шукану функцію:
Приклад 4. Визначити учасника злочину, виходячи з двох посилок:
1) "Якщо Іванов не брав участі або Петров брав участь, то Сидоров брав участь";
2) 2) "Якщо Іванов не брав участі, то Сидоров не брав участі".
I - "Іванов брав участь у злочині";
P - "Петров брав участь у злочині";
S - "Сидоров брав участь у злочині".
Запишемо посилки у вигляді формул:
Перевіримо результат, використовуючи таблицю істинності:
Відповідь: Іванов брав участь у злочині.
Кількість вхідних змінних в заданому виразі дорівнює трьом (A, B, C). Значить, кількість вхідних наборів Q = 2 3 = 8.
Стовпці таблиці істинності відповідають значенням вихідних виразів A, B, C. проміжних результатів і (B V C), а також шуканого остаточного значення складного арифметичного виразу:
1. Складемо таблицю істинності для формули. яка містить дві змінні x і y. У перших двох стовпчиках таблиці запишемо чотири можливих пари значень цих змінних, в наступних стовпцях - значення проміжних формул і в останньому стовпці - значення формули. В результаті отримаємо таблицю:
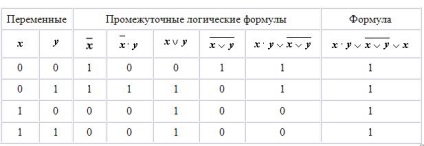
З таблиці видно, що при всіх наборах значень змінних x і y формула приймає значення 1, тобто є тотожно істинною.
2. Таблиця істинності для формули
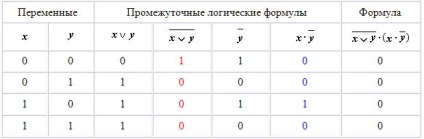
3. Таблиця істинності для формули:

З таблиці видно, що формула в деяких випадках приймає значення 1, а в деяких - 0, тобто є здійсненним.
Вася запитав у мами: «Можна піти в кіно або на футбол?» Мама відповіла негативно. Як вчинити хлопчикові?
Перевіримо правильність цього закону за допомогою таблиці істинності.
У класі виявилося розбите скло. Учитель пояснює директору: це зробив Коля або Саша. Але Саша цього на робив, тому що в цей час здавав мені залік. Отже, це зробив Коля
Рішення: Формалізуємо дане складне висловлювання.
К - це зробив Коля
С - це зробив Саша
Кількість простих висловлювань n = 2.