Список літератури. 15
Масиви і пов'язані списки визначають колекції об'єктів, доступ до яких здійснюється послідовно. Такі структури даних називають лінійними (linear) списками, оскільки вони мають унікальні перший і останній елементи і у кожного внутрішнього елемента є тільки один спадкоємець. Лінійний список є абстракцією, що дозволяє маніпулювати даними, що подаються по-різному - масивами, стеками, чергами і зв'язаними списками.
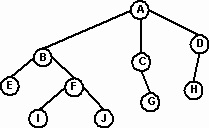
У багатьох додатках виявляється нелінійний порядок об'єктів, де елементи можуть мати кількох спадкоємців. Наприклад, в фамільному дереві батько може мати кількох нащадків (дітей). На Рис. 1 показані три покоління родини. Таке впорядкування називають ієрархічним.
У цій статті ми розглянемо нелінійну структуру, яка називається деревом (tree), яка складається з вузлів і гілок і має напрямок від кореня до зовнішніх вузлів, званим листям. Ці структури подібні комунікаційної мережі, показаної на Рис. 2, вимагають особливих алгоритмів і застосовуються в спеціальних додатках.
Деревоподібна структура характеризується великою кількістю вузлів (nodes), що походять від єдиного початкового вузла, званого коренем (root). На Рис. 3 коренем є вузол А. В термінах генеалогічного дерева вузол можна вважати батьком (parent), що вказує на 0, 1 або більше вузлів, званих синами (children). Наприклад, вузол В є батьком синів E і F. Батько вузла H - вузол D. Дерево може представляти кілька поколінь родини. Сини вузла і сини їхніх синів називаються нащадками (descendants), а батьки і прабатьки - предками (ancestors) цього вузла. Наприклад, вузли E, F, I, J - нащадки вузла B. Кожен некорневой вузол має тільки одного з батьків, і кожен батько має 0 або більше синів. Вузол, що не має дітей (E, G, H, I, J), називається листом (leaf).
Кожен вузол дерева є коренем піддерева (subtree), яке визначається цим вузлом і всіма нащадками цього вузла. Вузол F є корінь поддерева, що містить вузли F, I і J. вузол G є коренем піддерева без нащадків. Це визначення дозволяє говорити, що вузол A є корінь поддерева, яка сама виявляється деревом.
Перехід від батьківського вузла до дочірнього і до інших нащадкам здійснюється уздовж шляху (path). Наприклад, на Рис. 4 шлях від кореня A до вузла F проходить від A до B і від B до F. Той факт, що кожен некорневой вузол має єдиного батька, гарантує, що існує єдиний шлях з будь-якого вузла до його нащадкам. Довжина шляху від кореня до цього вузла є рівень вузла. Рівень кореня дорівнює 0. Кожен син кореня є вузлом 1-го рівня, наступне покоління - вузлами 2-го рівня і т.д. Наприклад, на Рис. 4 вузол F є вузлом 2-го рівня з довжиною шляху 2.
Глибина (depth) дерева є його максимальний рівень. Поняття глибини також може бути описане в термінах шляху. Глибина дерева є довжина найдовшого шляху від кореня до вузла.
На Рис.4 глибина дерева дорівнює 3.
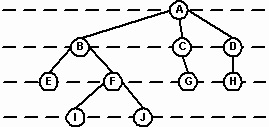
Рис.4. Рівень вузла і довжина шляху
Хоча дерева загального вигляду досить важливі, ми зосередимося на обмеженому класі дерев, де кожен батько має не більше двох синів (Рис. 5). Такі бінарні дерева (binary trees) мають уніфіковану структуру, яка допускає різноманітні алгоритми проходження і ефективний доступ до елементів. Вивчення бінарних дерев дає можливість вирішувати найбільш загальні завдання, пов'язані з деревами, оскільки будь-яке дерево загального вигляду можна уявити еквівалентним йому бінарним деревом.
У кожного вузла бінарного дерева може бути 0, 1 або 2 сина. По відношенню до вузла зліва будемо вживати термін лівий син (left child), а по відношенню до вузла справа - правий син (right child). Найменування "лівий" і "правий" відносяться до графічного поданням дерева. Бінарне дерево є рекурсивної структурою. Кожен вузол - це корінь свого власного поддерева. У нього є сини, які самі є корінням дерев, званих лівим і правим піддеревами відповідно. Таким чином, процедури обробки дерев рекурсивних. Ось рекурсивне визначення бінарного дерева:
Бінарне дерево - це таке безліч вузлів B, що
а) B є деревом, якщо безліч вузлів порожньо (пусте дерево - теж дерево);
б) B розбивається на три непересічних підмножини:
· Ліве піддерево R
· Праве піддерево R
На будь-якому рівні n бінарне дерево може містити від 1 до 2n вузлів. Число вузлів, що припадає на рівень, є показником щільності дерева. Інтуїтивно щільність є міра величини дерева (число вузлів) по відношенню до глибини дерева. На Рис. 5 дерево А містить 8 вузлів при глибині 3, в той час як дерево B містить 5 вузлів при глибині 4. Останній випадок є особливою формою, званої виродженим (degenerate) деревом, у якого є єдиний лист (E) і кожен нелістовой вузол має тільки одного сина. Вироджене дерево еквівалентно пов'язаному списку.
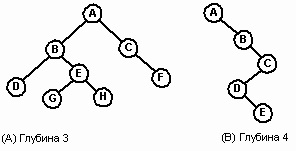
Рис.5. бінарні дерева
Дерева з великою щільністю дуже важливі в якості структур даних, так як вони містять пропорційно більше елементів поблизу кореня, тобто з більш короткими шляхами від кореня. Щільне дерево дозволяє зберігати великі колекції даних і здійснювати ефективний доступ до елементів. Швидкий пошук - головне, що обумовлює використання дерев для зберігання даних.
Вироджені дерева є крайнім заходом щільності. Інша крайність - закінчені бінарні дерева (complete binary tree) глибини N, де кожен рівень 0. N - 1 має повний набір вузлів, і все листя рівня N розташовані зліва. Закінчена бінарне дерево, що містить 2N вузлів на рівні N, є повним. На Рис. 6 показані закінчене і повне бінарні дерева.
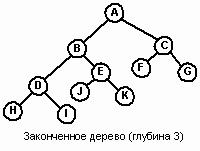
Рис.6. Класифікація бінарних дерев
Бінарні дерева класифікуються за кількома ознаками. Введемо поняття ступеня вузла і ступеня дерева. Ступенем вузла в дереві називається кількість дуг, яке з нього виходить. Ступінь дерева дорівнює максимальному ступені вузла, що входить в дерево. Виходячи з визначення ступеня зрозуміло, що ступінь вузла бінарного дерева не перевищує числа два. При цьому листям в дереві є вершини, що мають ступінь нуль.

Рис.7. бінарне дерево
Іншою важливою ознакою структурної класифікації бінарних дерев є строгість бінарного дерева. Строго бінарне дерево складається тільки з вузлів, що мають ступінь два або ступінь нуль. Нестрого бінарне дерево містить вузли зі ступенем дорівнює одному.

Рис.8. Повне і неповне бінарні дерева

Рис.9. Строго і не строго бінарні дерева
Бінарні дерева досить просто можуть бути представлені у вигляді списків або масивів. Списочное уявлення бінарних дерев засноване на елементах, відповідних вузлів дерева. Кожен елемент має поле даних і два поля покажчиків. Один покажчик використовується для зв'язування елемента з правим нащадком, а інший з лівим. Листя мають порожні покажчики нащадків. При такому способі подання дерева обов'язково слід зберігати покажчик на вузол, який є коренем дерева.
Можна помітити, що такий спосіб представлення має схожість з простими лінійними списками. І ця подібність не випадково. Насправді розглянутий спосіб представлення бінарного дерева є різновидом мультіспіска, утвореного комбінацією безлічі лінійних списків. Кожен лінійний список об'єднує вузли, що входять в шлях від кореня дерева до одного з листів.

Рис.10. Подання бінарного дерева у вигляді списковому структури
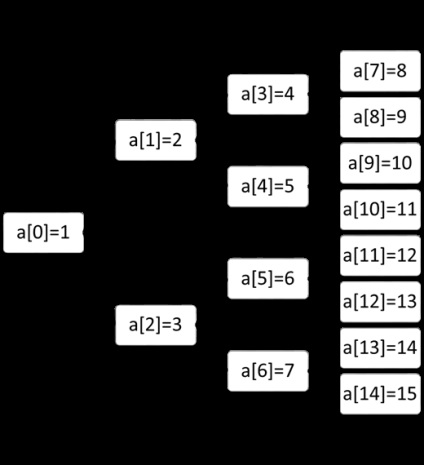
У вигляді масиву найпростіше представляється повне бінарне дерево, так як воно завжди має чітко визначена кількість вершин на кожному рівні. Вершини можна пронумерувати зліва направо послідовно за рівнями і використовувати ці номери в якості індексів в одновимірному масиві.

Рис.11. Подання бінарного дерева у вигляді масиву
Якщо число рівнів дерева в процесі обробки не буде істотно змінюватися, то такий спосіб представлення повного бінарного дерева буде значно економічнішим, ніж будь-яка спискові структура.
Головним недоліком розглянутого способу представлення бінарного дерева є те, що структура даних є статичною. Розмір масиву вибирається виходячи з максимально можливої кількості рівнів бінарного дерева. Причому чим менше повним є дерево, тим менш раціонально використовується пам'ять.
Як приклад використання бінарного дерева у вигляді масиву був використаний масив - a [i], що складається з 15 елементів (від 1 до 15). В результаті дерево повинно мати вигляд: