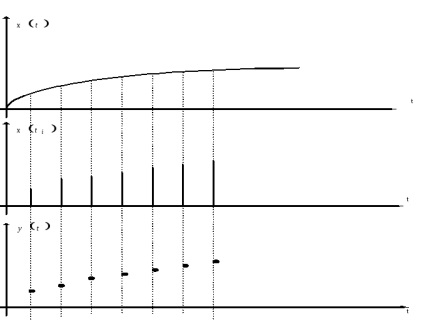
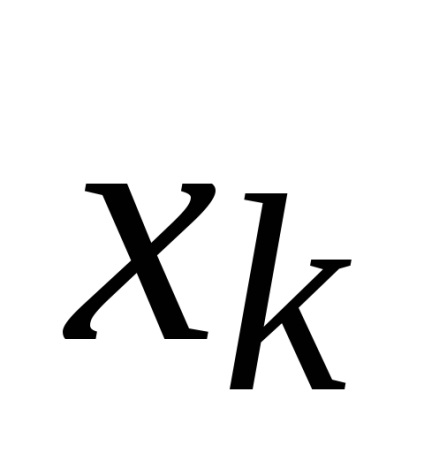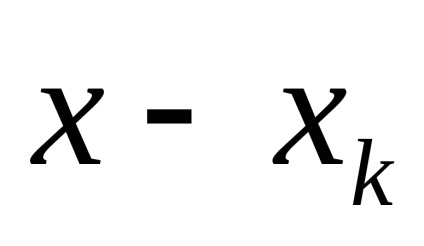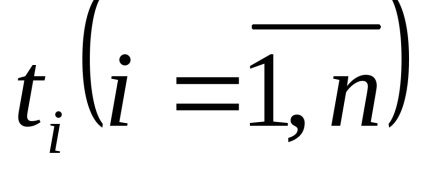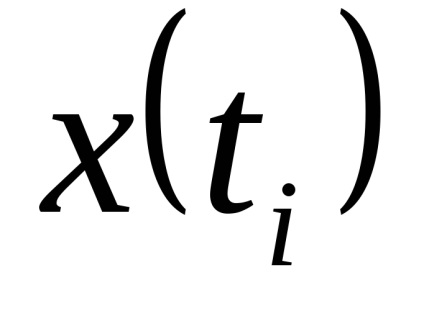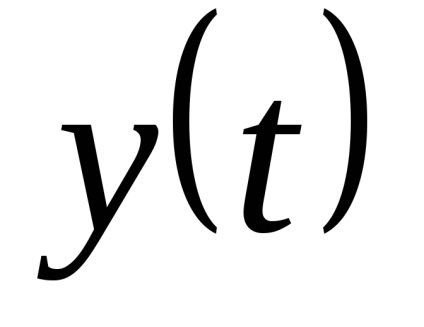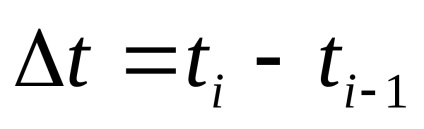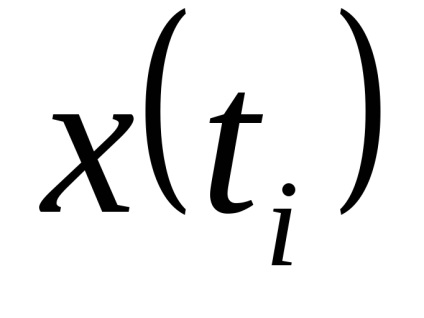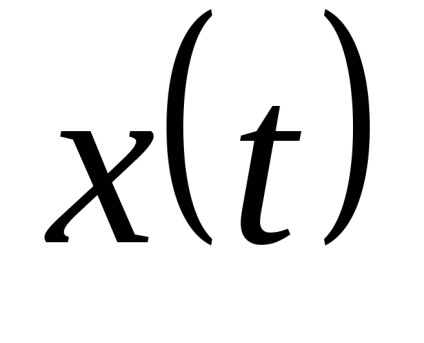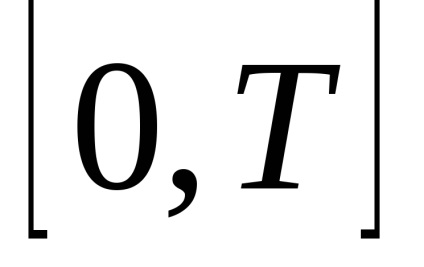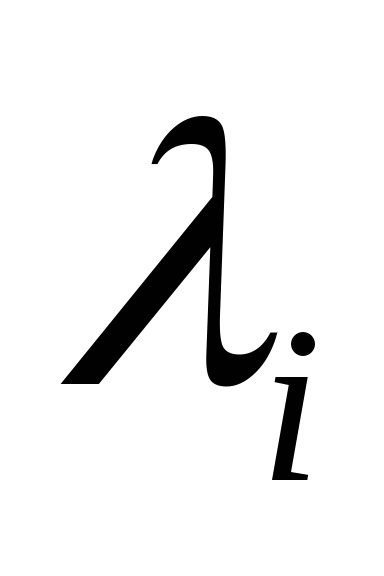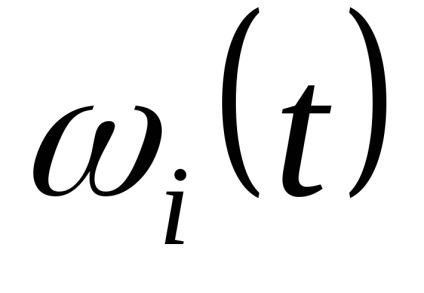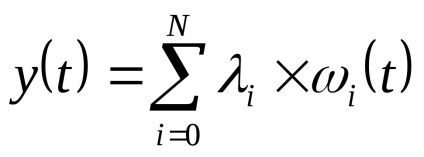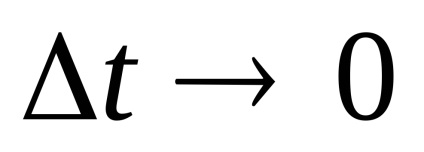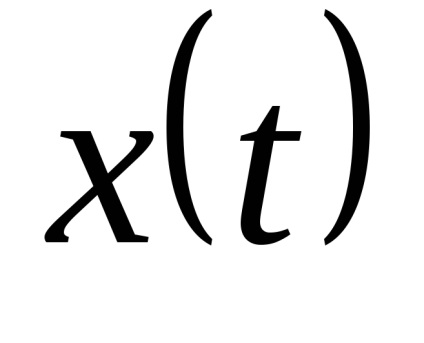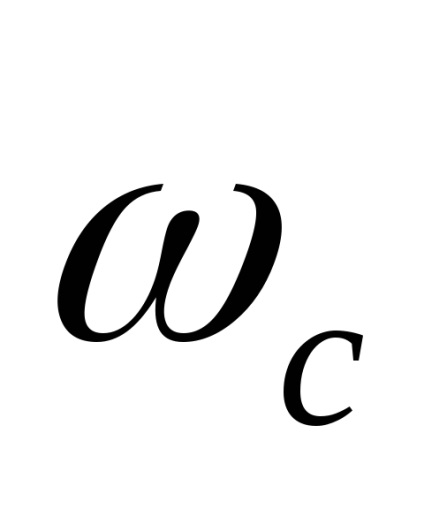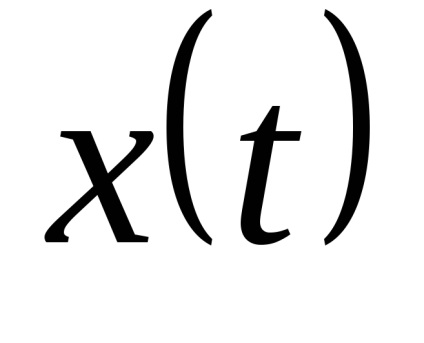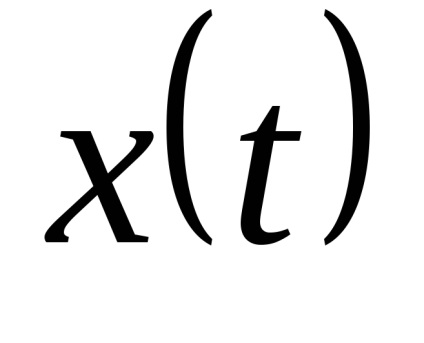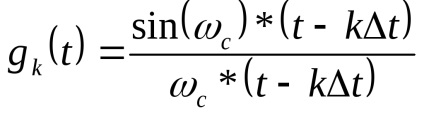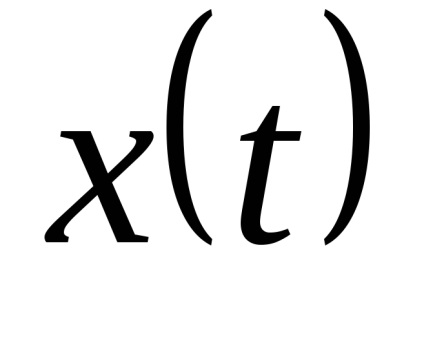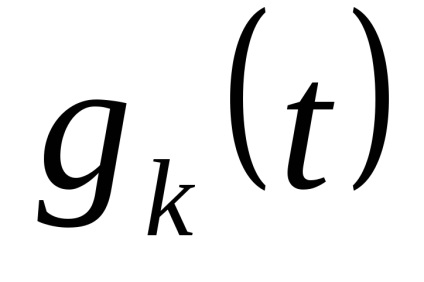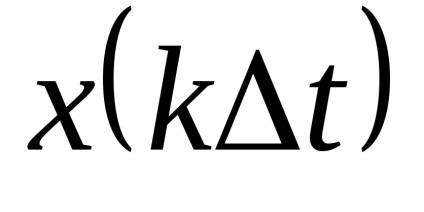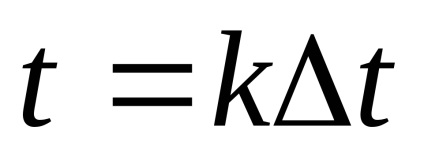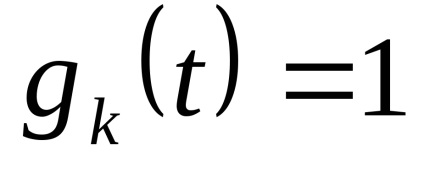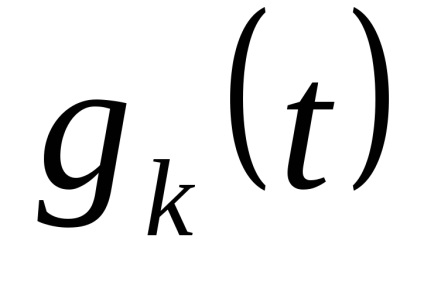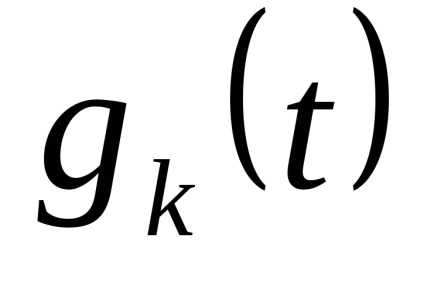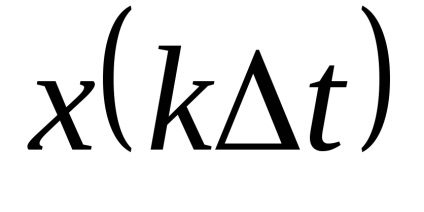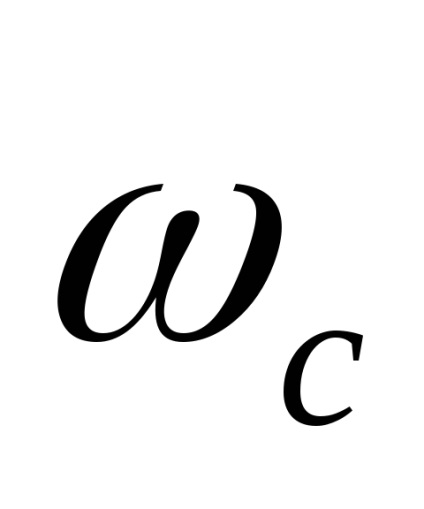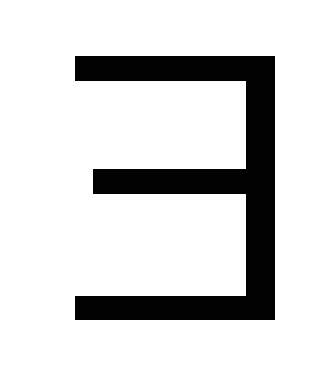Закон розподілу х іх випадковий. Як рівнів квантування найкраще брати середини відрізків розбиття. (Показати!)
Залежно від способу перетворення ЦИП діляться на прилади прямого і врівноважує перетворення.
У ЦИП прямого перетворення відсутня загальна зворотний зв'язок. Вони мають дуже велику швидкодію, але їх точність висока тільки при високій точності всіх перетворювачів.
ЦИП врівноважує перетворення охоплений загальною зворотним зв'язком. Перетворювач зворотного зв'язку ЦАП вихідного дискретного сигналу в компенсуючу величину хk однієї фізичної природи з вимірюваноївеличиною x (t). ЦАП виготовляється з елементів високої точності і стабільності.
Бувають прилади розгортає і слідкуючого врівноваження.
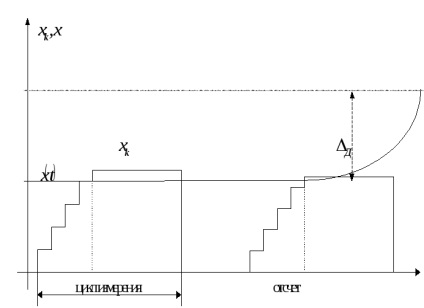
Для першого етапу значення компенсує величини
в кожному циклі вимірювання зростає від нуля ступенями, рівними кроці квантування. При досягненні рівності процес урівноваження припиняється, і фіксується результат вимірювання, що дорівнює числу ступенів квантування компенсує величини. Відлік показань зазвичай проводиться в кінці циклу.
Виникає динамічна похибка д.
В
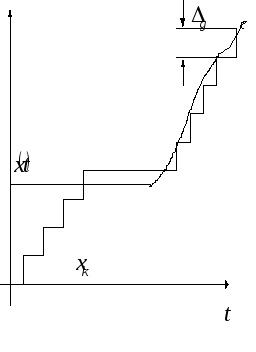
приладах слідкуючого врівноваження рівень компенсує величини не повертається до нуля, а залишається постійним. При зміні х відстежується, щоб
не перевищувала значення кроку квантування. Відлік проводитися або в момент врівноваження або за зовнішніми командам. Це складніше в технічному відношенні.
6.3. Дискретизація за часом і відновлення безперервних функцій.
Є кілька способів дискретизації.
Перехід від функції безперервного часу до функції дискретного часу може бути виконаний шляхом взяття відліків функції в певні дискретні моменти часу
. за відліком
можна відновити іншу функцію (шукану)
, яка б відтворювала вихідну із заданою точністю. При дискретизації за часом одним з найважливіших є питання про вибір кроку дискретизації:
.
Існує оптимальний крок дискретизації, який забезпечує відновлення вихідної функції з заданою точністю при мінімальному числі відліків
на кінцевому інтервалі часу.
безперервна функція
на інтервалі спостереження
замінюється кінцевим числом коефіцієнтів розкладання
на обраній системі базисних функцій
Зручність цієї системи.
Можна припустити, що точне відновлення вихідної неперервної функції в часі можливо лише при
. Однак існує широкий клас процесів, для яких можливо точне відновлення при кінцевому значенні кроку дискретизації. До даного класу відносяться сигнали з обмеженим спектром.
6.3.1. Теорема Котельникова.
Якщо безперервна функція
задовольняє умовам Дирихле (обмежена, кусково-неперервна і має кінцеве число екстремумів), і її спектр обмежений деякою частотою
(Частота зрізу), то існує такий мінімальний інтервал
між відліками, при якому є можливість безпомилково відновити діскретізіруемую функцію
по дискретним відліком. Цей максимальний інтервал:
Заснована теорема на можливості розкладання функції
в ряд:
функція відліків (6.7)
Тобто функцію
можна розкласти по системі базисних функцій
. Причому коефіцієнти разложеніязначенія
в дискретні моменти часу.
при
max значення
функції
ортогональні на нескінченно великому інтервалі часу.
Практична цінність розкладання функції в ряд Котельникова полягає в тому, що каналу зв'язку не передаються відомі по виду функції відліків
, а передаються тільки гратчасті функції
.
З точки зору практичної реалізації функція відліків повністю відповідає зміні в часі напруги на виході ідеального фільтра нижніх частот, однаково пропускає всі частоти від 0 до
, при подачі на його вхід
імпульса.
В реальних умовах точне відновлення неможливе через те, що не виконуються умови теореми Котельникова.
реальні функція
на кінцевих інтервалах часу, тому їх спектри нескінченні.
Схожі статті