Знайдемо визначник отриманої матриці.
# 8710; 3 = (-1) 1 + 1a11 # 8710; 11 + (-1) 2 + 1a21 # 8710; 21 + (-1) 3 + 1a31 # 8710; 31 = 16 • (3 • (-28) - (- 1) • 44) -10 • (2 • (-28) - (- 1) • (-14)) + 6 • (2 • 44-3 • (-14)) = 840
Випишемо окремо знайдені змінні Х
В) за допомогою оберненої матриці.
Позначимо через А - матрицю коефіцієнтів при невідомих; X - матрицю-стовпець невідомих; B - матрицю-стовпець вільних членів:, Вектор B: BT = (- 14,44, -28)
З урахуванням цих позначень дана система рівнянь приймає наступну матричну форму: А * Х = B.
Якщо матриця А - невироджена (її визначник відмінний від нуля, то вона має обернену матрицю А-1. Помноживши обидві частини рівняння на А-1, отримаємо: А-1 * А * Х = А-1 * B, А-1 * А = Е.
Це рівність називається матричної записом рішення системи лінійних рівнянь. Для знаходження рішення системи рівнянь необхідно обчислити обернену матрицю А-1.
Система буде мати рішення, якщо визначник матриці A відмінний від нуля.
Знайдемо головний визначник.
Отже, визначник 140 ≠ 0, тому продовжуємо рішення. Для цього знайдемо обернену матрицю через алгебраїчні доповнення.
Нехай маємо невироджених матрицю А:
Де Aij - алгебраїчне доповнення елемента aij в визначнику матриці А, яке є твором (-1) i + j на мінор (визначник) N-1 порядку, отриманий викреслюванням I-го рядка і J-го стовпця в визначнику матриці А.
Транспонована матриця до матриці A має вигляд:
Обчислюємо алгебраїчні доповнення.
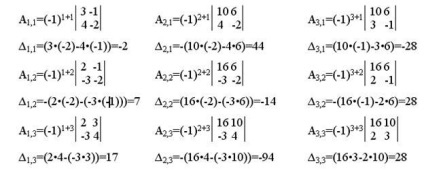
З отриманих алгебраїчних доповнень складемо приєднану матрицю:
Обчислимо зворотну матрицю:
Вектор результатів X X = A-1 • B