

Покрокове рішення задачі №10 - перетин кругового тора і циліндра
Завдання № 10 так само присвячена темі побудови лінії перетину поверхонь - тора і циліндра. Це найбільш складні і трудомісткі завдання, що вимагають знання методів побудови ліній перетину різних поверхонь.
Для вирішення завдань необхідно знати:
- способи завдання поверхні на комплексному кресленні;
- методи побудови лінії перетину поверхонь в задачах з нарисної геометрії:
а) метод січної площини;
б) метод утворюють;
в) метод кульового посередника (концентричних і ексцентричних куль).
Порядок вирішення Завдання
1. Відповідно до варіанту завдання по координатам точок будуємо в двох проекціях поверхні прямого кругового циліндра і відкритого тора (четверта його частина) в тонких лініях або як на рис. 10.1.
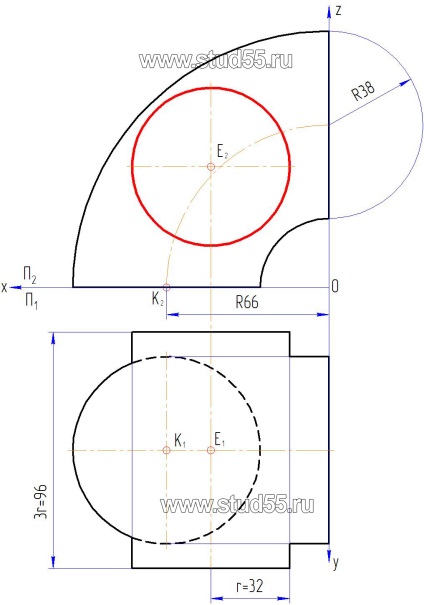
2. Для побудови лінії перетину застосовуємо метод утворюють (метод січної площини розглянуто раніше), як найбільш відповідний стосовно до цього завдання. Суть його полягає в тому, що на поверхні, яка представлена в загальному вигляді, проводиться ряд утворюють, відзначаються точки перетину цих утворюють з другої поверхнею, яка задана лінією перетину цих поверхонь (вона є фронтально-проектує). Далі знаходяться проекції цих утворюють і проекції точок лежать на них на сполученої площині проекцій. Поєднуючи їх плавною лінією, отримуємо шукану лінію перетину заданих поверхонь.
Отже, в завданню необхідно побудувати лінію перетину прямого кругового циліндра і торів поверхні (одна четверта частина відкритого тора). Завдання вирішується в такій послідовності:
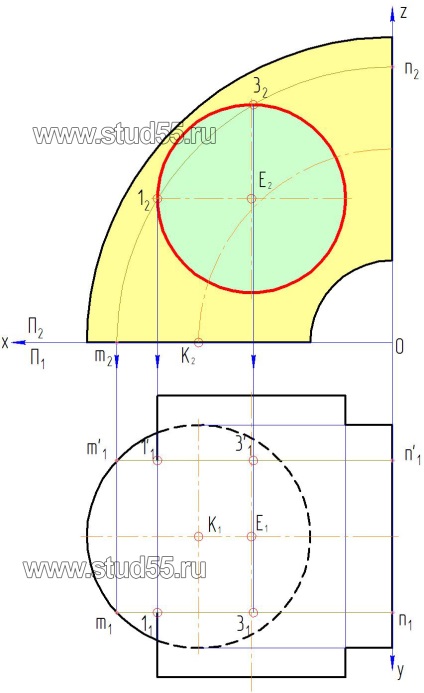
а) проводимо першу творчу m2n2 у фронтальній площині проекцій П2 по торів поверхні. Відзначаємо проекції точок перетину її з циліндричною поверхнею 12 = 1'2 і 32 = 3'2. В якості точки 12 беремо точку дотику циліндричної поверхні з крайньої лівої утворює тора (див. Рис. 10.2);
в) переносимо (проектуємо) точки перетину утворює з циліндричної поверхні фронтальної площини на горизонтальну площину, отримуємо 12 -1'2 і 32 -3'2. Це і є проекції точок, що належать лінії перетину поверхонь, тому що вони одночасно належать (перебувають) на торів і циліндричної поверхнях.
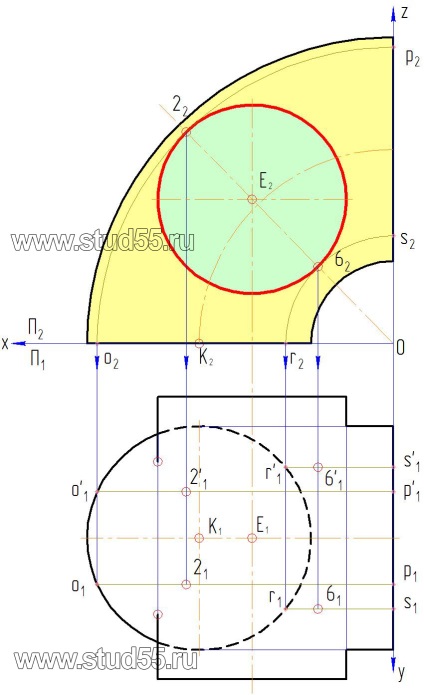
Для отримання наступних двох пар точок проводимо ще дві утворюють o2p2іr2s2 по верхній і нижній дотичній з циліндричною поверхнею в точці 22 і 62. Щоб отримати проекції точок на П2. необхідно через початок проекцій 0 і центр Е2 провести пряму лінію, і в місцях, де вона перетне контур поверхні циліндра, одержимо шукані проекції точок 2 і 6. Повторюємо всі дії, викладені в пунктах «а», «б», «в».
г) далі проводимо утворюють через вибраний інтервал або через характерні (опорні) точки поверхонь, в даному прикладі через опорні точки (рис. 10.3).
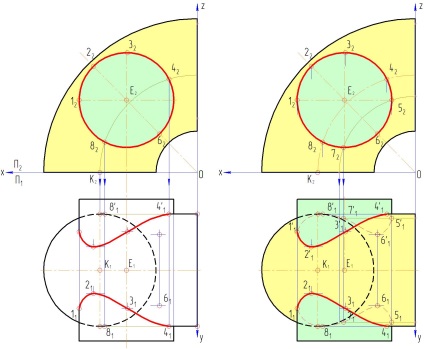
3. Отримані проекції точок в горизонтальній площині з'єднуємо послідовно по парній і непарній гілки плавною кривою з урахуванням видимості одночасно обох поверхонь, - це і буде лінія перетину заданих поверхонь. Видимість її визначається виходячи з того, що видимими точками будуть усі точки, горизонтальної проекції циліндричної поверхні, які у фронтальній проекції знаходяться вище діаметра циліндра. Для торів поверхні видимими будуть точки в горизонтальній проекції, які у фронтальній - розташовуються вище і лівіше осі тора (вісь тора, також як і діаметр циліндра є межами видимості). Решта точки як для циліндра, так і для тора будуть невидимими (рис. 10.4).
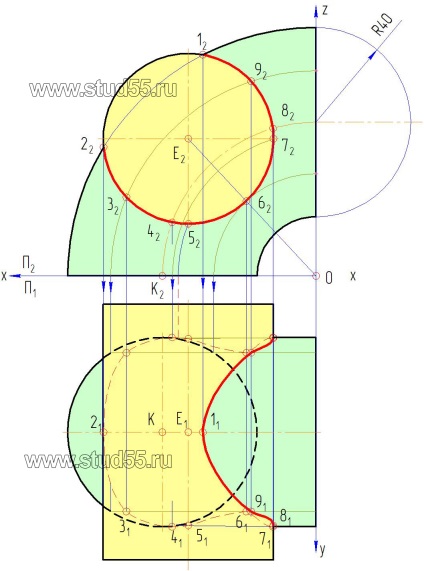
4. Слід зауважити, як зазначалося раніше, що перетин поверхонь може бути повним і неповним. При неповному перетині - лінія перетину є одна замкнута петля (розглянутий приклад завдання), при повному перетині - лінія перетину розпадається на кілька замкнутих петель (в основному дві). Будівництво їх здійснюється таким же методом, як викладено в цій задачі.
Після побудови лінії перетину поверхонь остаточно відводяться контурними лініями видима частина лінії перетину і відповідні видимі контури поверхонь; невидимими (штриховими) лініями відводяться всі інші лінії.
Розділ: Нарисна геометрія /