Поліноміальна інтерполяція функції f (x) на відрізку [a, b] - побудова многочлена Pn (x) ступеня меншою або рівною n. приймає у вузлах інтерполяції x0. x1. xn значення f (xi):
P n (x i) = a 0 + a 1 x i + a 2 x i 2 +. + A n x i n = f (x i). i = 0. 1. n (x _) = a_ + a_x_ + a_x _ ^ +. + A_x _ ^ = f (x _), \ quad i = 0,1. n>
Він відмінний від нуля при всяких попарно різних значеннях xi. і інтерполювання функції f по її значеннях в вузлах xi за допомогою многочлена Pn (x) завжди можливо і єдино.
Отриману інтерполяційну формулу f (x) ≈ P n (x) (x)> часто використовують для наближеного обчислення значень функції f при значеннях аргументу x. відмінних від вузлів інтерполяції. При цьому розрізняють інтерполювання у вузькому сенсі, коли x ∈ [x 0. x n], x_ \ right]>. і екстраполірованіе. коли x ∈ [a. b]. x ∉ [x 0. x n], x_ \ right]>
Нехай в просторі задані n точок P 1. P 2. .... P n, P _, \ dots, P_>. які в деякій системі координат мають радіус-вектори r 1. r 2. .... r n _, \ mathbf _, \ dots, \ mathbf _>.
Завдання інтерполяції полягає в побудові кривої, що проходить через зазначені точки в зазначеному порядку.
Через фіксований набір точок можна провести нескінченне число кривих, тому завдання інтерполяції не має однозначної відповіді.
Введення параметризації і сітки може бути виконано різними способами. Зазвичай вибирають або рівномірну сітку, вважаючи a = 0. b = n - 1. t i = i - 1 = i-1>. або, що більш переважно, з'єднують точки відрізками і як різниці значень параметра t i + 1 - t i -t_> беруть довжину відрізка r i + 1 - r i _- \ mathbf _>.
Одним з поширених способів інтерполяції є використання кривої у вигляді многочлена від t ступеня n - 1. тобто у вигляді функції
Ці умови призводять до системи лінійних рівнянь для коефіцієнтів a k>
(1 t 1 t 1 2 ... t 1 n - 1 1 t 2 t 2 2 ... t 2 n - 1 ⋮ ⋮ ⋮ ⋮ 1 tntn 2 ... tnn - 1) (anan - 1 ⋮ a 1) = (r 1 r 2 ⋮ rn) 1t_t _ ^ \ ldots t _ ^ \\ 1t_t _ ^ \ ldots t _ ^ \\\ vdots \ vdots \ vdots \ Vdots \\ 1t_t _ ^ \ ldots t _ ^ \ end> \ mathbf _ \\\ mathbf _ \\\ vdots \\\ mathbf _ \ end> = \ mathbf _ \\\ mathbf _ \\\ vdots \\\ mathbf _ \ end >>Звернемо увагу, що потрібно вирішити три системи рівнянь: для x. y і z координат. Всі вони мають одну матрицю коефіцієнтів, звертаючи яку, за значеннями радіус-векторів r i _> точок обчислюються вектори a k> коефіцієнтів многочлена. визначник матриці
W (t 1. t 2. .... T n) = | 1 t 1 t 1 2 ... t 1 n - 1 1 t 2 t 2 2 ... t 2 n - 1 ⋮ ⋮ ⋮ ⋮ 1 t n t n 2 ... t n n - 1 | = Π i. j. i> j (t i - t j), t _, \ ldots, t _) = 1t_t _ ^ \ ldots t _ ^ \\ 1t_t _ ^ \ ldots t _ ^ \\\ vdots \ vdots \ vdots \ Vdots \\ 1t_t _ ^ \ ldots t _ ^ \ end> = \ prod _ (t_-t _)>
називається визначником Вандермонда. Якщо вузли сітки не збігаються, він відмінний від нуля, так що система рівнянь має рішення.
Крім прямого звернення матриці, є кілька інших способів обчислення интерполяционного многочлена. В силу єдиності многочлена мова йде про різні форми його записи.
- Для заданого набору точок і сітки параметра крива будується однозначно.
- Крива є інтерполяційної, тобто проходить через всі задані точки.
- Крива має безперервні похідні будь-якого порядку.
- З ростом числа точок порядок многочлена зростає, а разом з ним зростає число операцій, яке потрібно виконати для обчислення точки на кривій.
- З ростом числа точок у інтерполяційної кривої можуть виникнути осциляції (див. Приклад нижче).
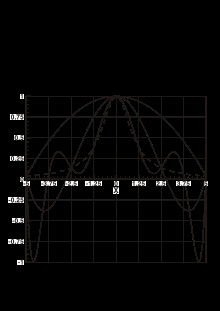
Інтерполяція на послідовності сіток. Приклад Рунге.
Класичним прикладом (Рунге), що показує виникнення осциляцій у интерполяционного многочлена, служить інтерполяція на рівномірній сітці значень функції
який в точках x i> приймає значення y i = 1 / (1 + x i 2) = 1 / (1 + x _ ^)>. На малюнку представлені графіки самої функції (штрих-пунктирна лінія) і трьох інтерполяційних кривих при n = 3. 5. 9:
- інтерполяція на сітці x 1 = - 5. x 2 = 0. x 3 = 5 = -5, x_ = 0, x_ = 5> - квадратична парабола;
- інтерполяція на сітці x 1 = - 5. x 2 = - 2.5. x 3 = 0. x 4 = 2.5. x 5 = 5 = -5, x _ = - 2.5, x_ = 0, x_ = 2.5, x_ = 5> - многочлен четвертого ступеня;
- інтерполяція на сітці x 1 = - 5. x 2 = - 3.75. x 3 = - 2.5. x 4 = - 1.25. x 5 = 0. x 6 = 1.25. x 7 = 2.5. x 8 = 3.75. x 9 = 5 = -5, x _ = - 3.75, x _ = - 2.5, x _ = - 1.25, x_ = 0, x_ = 1.25, x_ = 2.5, x_ = 3.75, x_ = 5> - многочлен восьмому ступені.
Значення інтерполяційного многочлена навіть для гладких функцій в проміжних точках можуть сильно ухилятися від значень самої функції.