Політропний називається процес, який описується рівнянням:
Показник політропи n може приймати будь-які значення в межах від -∞ до + ∞, але для даного процесу він є постійною величиною.
З рівняння політропної процесу і рівняння Клайперона можна отримати вираз, що встановлює зв'язок між p, v і T в будь-яких двох точках на політропи:
Робота розширення газу в Політропний процесі дорівнює:
У разі ідеального газу цю формулу можна перетворити:
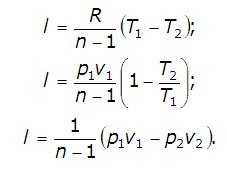
Кількість підведеної або відведеної в процесі теплоти визначається за допомогою першого закону термодинаміки:
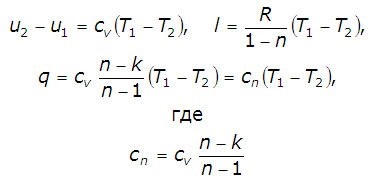
є теплоємність ідеального газу в Політропний процесі.
При cv. k і n = const cn = const, тому політропний процес іноді визначать як процес з постійною теплоємністю.
Політропний процес має узагальнююче значення, бо охоплює всю сукупність основних термодинамічних процесів.
Графічне представлення політропи в p, v координатах в залежності від показника політропи n.
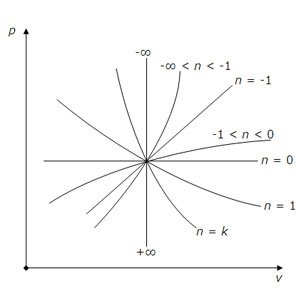
pv 0 = const (n = 0) - ізобара;
pv = const (n = 1) - ізотерма;
p 0 v = const, p 1 / ∞ v = const, pv ∞ = const - ізохора;
pv k = const (n = k) - адіабата.
n> 0 - гіперболічні криві,
n <0 – параболы.
Тепловим двигуном називається пристрій, здатний перетворювати отриману кількість теплоти в механічну роботу. Механічна робота в теплових двигунах виробляється в процесі розширення деякого речовини, яке називається робочим тілом. Як робоче тіло зазвичай використовуються газоподібні речовини (пари бензину, повітря, водяна пара). Робоче тіло отримує (або віддає) теплову енергію в процесі теплообміну з тілами, що мають великий запас внутрішньої енергії. Ці тіла називаються тепловими резервуарами.
Як випливає з першого закону термодинаміки, отримане газом кількість теплоти Q повністю перетворюється в роботу A при ізотермічному процесі, при якому внутрішня енергія залишається незмінною (# 916; U = 0):
Але такий одноразовий акт перетворення теплоти в роботу не представляє інтересу для техніки. Реально існуючі теплові двигуни (парові машини, двигуни внутрішнього згоряння і т. Д.) Працюють циклічно. Процес теплопередачі і перетворення отриманої кількості теплоти в роботу періодично повторюється. Для цього робоче тіло повинне здійснювати круговий процес або термодинамічний цикл, при якому періодично відновлюється початковий стан. Кругові процеси зображуються на діаграмі (p, V) газоподібного робочого тіла за допомогою замкнутих кривих (рис. 3.11.1). При розширенні газ здійснює позитивну роботу A1. рівну площі під кривою abc, при стисненні газ робить негативну роботу A2. рівну по модулю площі під кривою cda. Повна робота за цикл A = A1 + A2 на діаграмі (p, V) дорівнює площі циклу. Робота A позитивна, якщо цикл обходиться за годинниковою стрілкою, і A негативна, якщо цикл обходиться в протилежному напрямку.
Малюнок 3.11.1. Круговий процес на діаграмі (p, V). abc - крива розширення, cda - крива стиснення. Робота A в круговому процесі дорівнює площі фігури abcd
Загальна властивість всіх кругових процесів полягає в тому, що їх неможливо провести, приводячи робоче тіло в тепловий контакт тільки з одним тепловим резервуаром. Їх потрібно, принаймні, два. Тепловий резервуар з більш високою температурою називають нагрівачем, а з більш низькою - холодильником. Здійснюючи круговий процес, робоче тіло отримує від нагрівача деяку кількість теплоти Q1> 0 і віддає холодильнику кількість теплоти Q2 <0. Полное количество теплоты Q, полученное рабочим телом за цикл, равно
При обході циклу робоче тіло повертається в первісний стан, отже, зміна його внутрішньої енергії дорівнює нулю (# 916; U = 0). Відповідно до першого закону термодинаміки,
Модель. термодинамічні цикли
Коефіцієнт корисної дії вказує, яка частина теплової енергії, отриманої робочим тілом від «гарячого» теплового резервуара, перетворилася в корисну роботу. Інша частина (1 - # 951;) була «марно» передана холодильника. Коефіцієнт корисної дії теплової машини завжди менше одиниці (# 951; <1). Энергетическая схема тепловой машины изображена на рис. 3.11.2.
Малюнок 3.11.2. Енергетична схема теплової машини: 1 - нагрівач; 2 - холодильник; 3 - робоче тіло, що здійснює круговий процес. Q1> 0, A> 0, Q2 <0; T1> T2
У двигунах, що застосовуються в техніці, використовуються різні кругові процеси. На рис. 3.11.3 зображені цикли, які використовуються в бензиновому карбюраторному і в дизельному двигунах. В обох випадках робочим тілом є суміш парів бензину або дизельного палива з повітрям. Цикл карбюраторного двигуна внутрішнього згоряння складається з двох изохор (1-2, 3-4) і двох адіабати (2-3, 4-1). Дизельний двигун внутрішнього згоряння працює по циклу, що складається з двох адіабати (1-2, 3-4), однієї ізобари (2-3) і однієї ізохорами (4-1). Реальний коефіцієнт корисної дії у карбюраторного двигуна близько 30%, у дизельного двигуна - близько 40%.
Малюнок 3.11.3. Цикли карбюраторного двигуна внутрішнього згоряння (1) і дизельного двигуна (2)
У 1824 році французький інженер С. Карно розглянув круговий процес, що складається з двох ізотерм і двох адіабати, який зіграв важливу роль у розвитку вчення про теплових процесах. Він називається циклом Карно (рис. 3.11.4).
Малюнок 3.11.4. цикл Карно
Цикл Карно робить газ, що знаходиться в циліндрі під поршнем. На ізотермічному ділянці (1-2) газ приводиться в тепловий контакт з гарячим тепловим резервуаром (нагрівачем), що має температуру T1. Газ ізотермічні розширюється, здійснюючи роботу A12. при цьому до газу підводиться деяку кількість теплоти Q1 = A12. Далі на адіабатичному ділянці (2-3) газ поміщається в адіабатичну оболонку і продовжує розширюватися за відсутності теплообміну. На цій ділянці газ здійснює роботу A23> 0. Температура газу при адіабатичному розширенні падає до значення T2. На наступному ізотермічному ділянці (3-4) газ приводиться в тепловий контакт з холодним тепловим резервуаром (холодильником) при температурі T2 На діаграмі (p, V) ця робота дорівнює площі циклу. Процеси на всіх ділянках циклу Карно передбачаються квазістатичного. Зокрема, обидва ізотермічних ділянки (1-2 і 3-4) проводяться при нескінченно малій різниці температур між робочим тілом (газом) і тепловим резервуаром (нагрівачем або холодильником). Як випливає з першого закону термодинаміки, робота газу при адіабатичному розширенні (або стисненні) дорівнює убутку # 916; U його внутрішньої енергії. Для 1 моля газу де T1 і T2 - початкова і кінцева температури газу. Звідси випливає, що роботи, вчинені газом на двох адіабатичних ділянках циклу Карно, однакові по модулю і протилежні за знаками За визначенням, коефіцієнт корисної дії # 951; циклу Карно єСхожі статті