Помилка оцінки - це відхилення отриманої оцінки від невідомого значення оцінюваної ймовірнісної характеристики випадкової величини.
Помилка оцінки сама по собі є випадковою величиною. Вона має нульове математичне сподівання (передбачається, що зміщення оцінки відсутній) і деяку ненульову дисперсію n 2. величина якої залежить від обсягу вибірки n. Чим більше обсяг вибірки n. тим менше дисперсія n 2 і тим точніше оцінка.
Зазвичай для характеристики помилки оцінки використовується корінь квадратний з дисперсії оцінки n 2. і ця величина n носить назву среднеквадратической помилки.
Оскільки среднеквадратическая помилка оцінки n заздалегідь не відома, вона також підлягає оцінюванню. Її оцінка позначається додаванням «кришечки»:
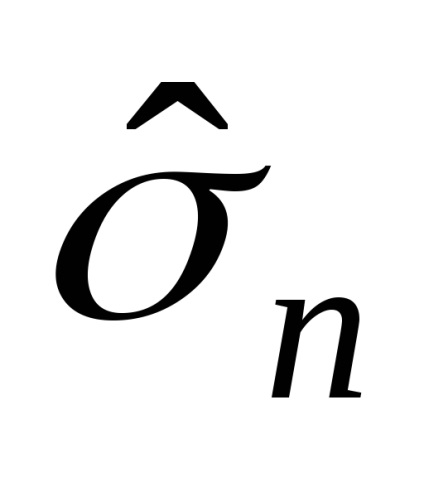
вибіркове середнє
Вибіркове середнє - це оцінка невідомого значення математичного очікування випадкової величини за вибірковими даними.
Обчислюється за формулою середнього арифметичного:
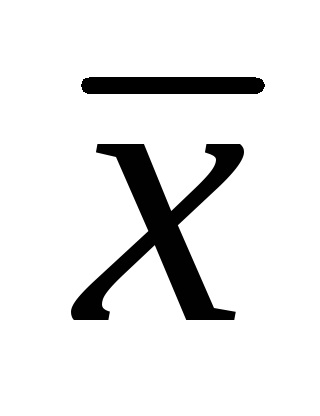
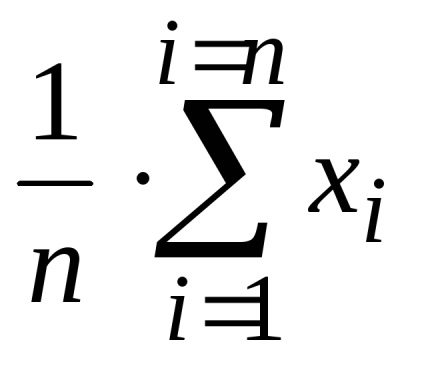
З ростом обсягу вибірки можливе відхилення вибіркового середнього
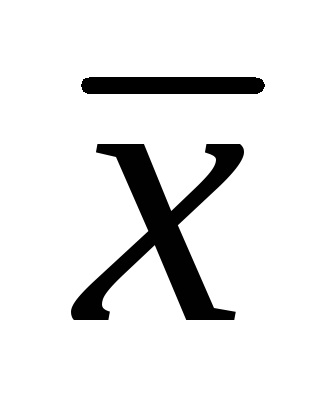
вибіркова дисперсія
Вибіркова дисперсія - це оцінка невідомого значення дисперсії спостерігається в досвіді випадкової величини.
Обчислюється за формулою середнього арифметичного, в якій вибіркові значення замінені квадратами відхилень вибіркових значень від математичного очікування. Як правило, математичне очікування генеральної сукупності невідомо, тому воно без великої помилки замінюється його оцінкою, тобто вибірковим середнім.
Таким чином, вибіркова дисперсія - це середній квадрат відхилення вибіркових значень від вибіркового середнього.
Формула для обчислення вибіркової дисперсії така:
s 2 = ((x1 -
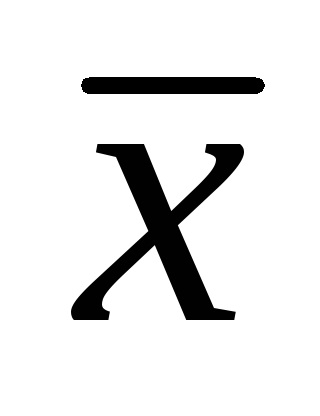
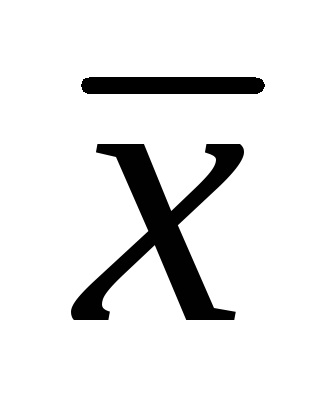
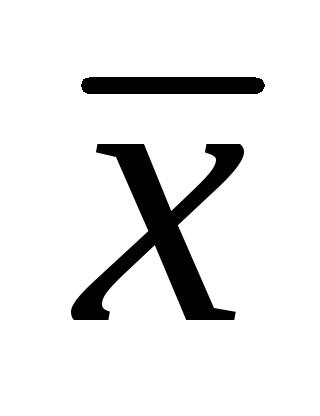
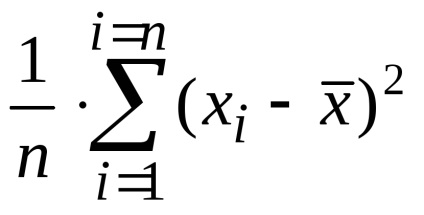
З ростом обсягу вибірки n можливе відхилення вибіркової дисперсії s 2 від оцінюваної невідомої дисперсії випадкової величини D (X) зменшується.
Вибіркове середньоквадратичне відхилення
Вибіркове середньоквадратичне відхилення - це оцінка невідомого значення середньоквадратичного відхилення (стандартного відхилення) спостерігається в досвіді випадкової величини.
Обчислюється як квадратний корінь з вибіркової дисперсії s 2.
Літерне позначення: s.
З ростом обсягу вибірки n можливе відхилення вибіркового середньоквадратичного відхилення s від оцінюваного середнє відхилення випадкової величини зменшується.
Вибіркова среднеквадратическая помилка
Вибіркова среднеквадратическая помилка - це обчислене за вибіркою відхилення отриманої оцінки від невідомого значення оцінюваної ймовірнісної характеристики випадкової величини.
Обчислюється як квадратний корінь з вибіркової дисперсії оцінки n 2.
З ростом обсягу вибірки n можливе значення вибіркової среднеквадратической помилки
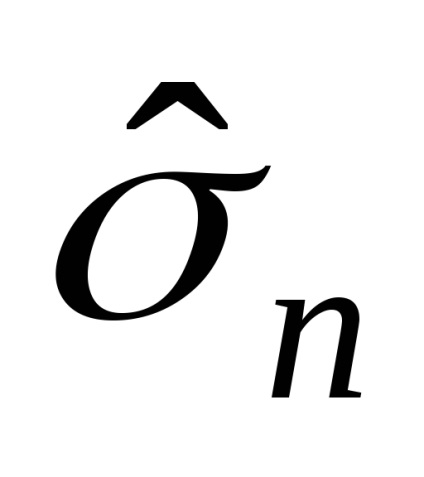
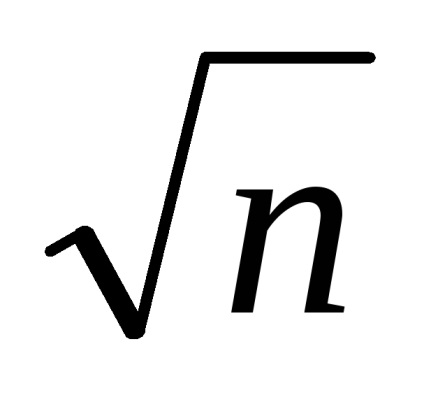
Вибірковий коефіцієнт кореляції
Вибірковий коефіцієнт кореляції - це оцінка невідомого значення коефіцієнта кореляції спостережуваних випадкових величин X і Y по парам вибіркових даних (x1. Y1), (x2. Y2), ..., (xn. Yn). Літерне позначення: r.
Вибірковий коефіцієнт кореляції показує ступінь тісноти статистичного зв'язку між відхиленнями вибіркових значень двох спостережуваних в досвіді випадкових величин X і Y від своїх математичних очікувань M (X) і M (Y), або, якщо вони не відомі, від вибіркових середніх
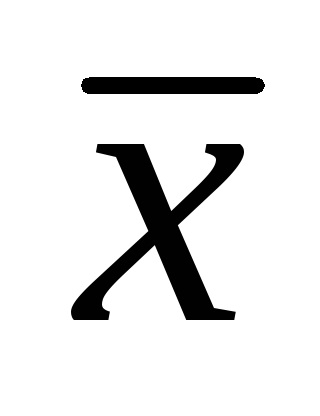

Формула для вибіркового коефіцієнта кореляції така:
З ростом обсягу вибірки n можливе відхилення вибіркового коефіцієнта кореляції r від оцінюваного невідомого коефіцієнта кореляції пари випадкових величин зменшується.