Всі ми в школі проходимо курс геометрії - науки, в якій хтось не бачить сенсу, а інші знаходять своє покликання. При цьому ми вивчаємо Евклидову геометрію, яка зародилася понад дві тисячі років тому, але і зараз залишається актуальною. Але майже всі чули і про інших, так званих неевклідових геометрії, зокрема - про геометрію Лобачевського. І найдивніше, що знайомство з цією наукою закінчувалося на твердженні, що вона допускає можливість перетину паралельних прямих. Цей факт дивує, навіть вражає, але, як і всі незрозуміле, сприймається на віру.
Але ж насправді геометрія Лобачевського не так вже сильно відрізняється від звичної нам геометрії і паралельні прямі в ній не перетинаються - це безпідставний міф, який народився за дивних обставин. Але, для того щоб це зрозуміти, необхідно хоча б коротко розібрати історію появи геометрії як науки.
У школах вивчається геометрія, основи якої були закладені давньогрецькими математиками. А приблизно в 300 році до н. е. світло побачив працю, що став основою всієї сучасної геометрії, - «Начала» Евкліда.
В «Засадах» зібрані всі геометричні відомості, отримані працями десятків математиків античності, що жили до Евкліда. Ця праця, що складається з тридцяти великих томів, на два тисячоліття став єдиним підручником, за яким можна було вивчити геометрію. І «Начала» прекрасно описують простір, в якому ми живемо, завдяки чому цю геометрію (як і простір) назвали Евклідовій.
Однак з кінця XVIII століття почалися спроби створення геометрії, відмінної від геометрії, описаної в «Засадах». Причиною тому стали суперечності, що виникають в Евклідовій геометрії, зокрема знаменита проблема п'ятого постулату. Наслідком цього постулату є поняття паралельних прямих, які не перетинаються, протягом всього шляху. саме
по собі це твердження не є чогось незвичайного або дивного, але в ньому є одна вада - довести його за допомогою математичного апарату просто-напросто неможливо! І саме ця обставина штовхнуло вчених на створення неевклідової геометрії, в якій даний недолік був би усунений.
Над зазначеною проблемою працювало кілька вчених, в тому числі і знаменитий Карл Гаусс, але «першопрохідцем» в цій області став російський математик Микола Лобачевський. Перша його робота, що заклала основи геометрії, відмінної від евклідової, з'явилася в 1829 році і з тих пір не зазнала особливих змін. Спочатку геометрія Лобачевського вважалася непридатною до практичного застосування, так як простір, в якому ми живемо, не відповідає простору, описуваного цієї геометрією. Однак закони, виведені Лобачевским, незабаром знайшли практичне застосування - стало можливим вирішення низки практичних завдань, практично не вирішуються за допомогою традиційних засобів.
Головна відмінність геометрії Лобачевського від геометрії Евкліда - в тому ж п'ятому постулаті. Саме через цю аксіоми багато людей помилково вважають, що неевклидова геометрія допускає перетин паралельних прямих. Однак це найглибша помилка, що народилося через невірне трактування постулату і деяких втрачених з уваги речей.
П'ятий постулат геометрії Лобачевського стверджує, що якщо на площині лежать пряма і точка, то через цю точку можна провести хоча б дві прямі, що не перетинаються з першої прямої. А в геометрії Евкліда через точку можна провести тільки одну-єдину пряму. Таким чином, неевклидова геометрія допускає, що на одній площині може перебувати відразу декілька прямих ліній, які не перетинаються один з одним.
А твердження про можливість перетину паралельних прямих в геометрії Лобачевського виникло через простого незнання аксіом цієї геометрії. Адже при найближчому розгляді виявляється, що в неевклідової геометрії не тільки не йдеться про перетин паралельних прямих, але й не йдеться про паралельні прямі взагалі - розмова тут йде саме про непересічних прямих, що знаходяться на одній площині.
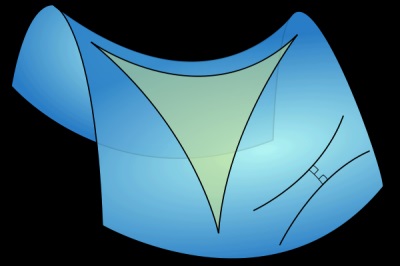
Щоб зрозуміти це, необхідно зробити одне дуже важливе уточнення: геометрія Лобачевського описує не плоске простір, як це робить геометрія Евкліда, а оперує поняттями гіперболічного простору. В геометрії Лобачевського простір не плоско, воно має деяку негативну кривизну. Уявити це досить складно, але гарною моделлю такого простору є геометричні тіла, схожі на воронку і сідло. І все сказане вище відноситься саме до поверхонь цих фігур.
Так що необхідно позбавитися від хибних понять про геометрію Лобачевського і зрозуміти, що вона може застосовуватися тільки по відношенню до світу з викривленим простором. Однак космологія (наука, що вивчає Всесвіт) в останні роки приходить до виходу, що простір, в якому ми живемо, може володіти негативною кривизною, найкращим чином описуваної саме геометрією Лобачевського.
27 плюсів 6 мінусів
- Кращі зверху
- перші зверху
- Актуальні зверху
kidont 1587 днів тому
Ось "трикутник" по Лобачевського, у якого сума кутів менше 180.
Розкрити гілка 3
rfrfirby 1 587 днів тому
дивно це, адже якщо площину розпрямити - то сума кутів буде 180, тобто повинні обумовлюватися умови вимірювання кутів. Повинні бути стандарти (норми). Адже і кривизна площині може бути різна - а трикутник може бути 1 накладений на різні площини.
Розкрити гілка 2
kidont 1587 днів тому
Картинкою Будь площину, а сідло.
Земний "куля", наприклад, теж не можна розпрямити в площину, тому карти містять певні спотворення.
Розкрити гілка 1
rfrfirby 1 587 днів тому
ога або ще варіант - де як часточки апельсина - тоді менше спотворень на площині, але розриви, але тоді і трикутник буде перериватися або навпаки будуть надлишки ліній о_0 в залежності від увігнута або опукла поверхня, в загальному треба буде порозбирали в цій темі -_-