Крім основних факторів, вплив яких на об'єкт дослідження вивчається при проведенні експерименту, діють випадкові чинники. Неідеальні умови проведення дослідів призводять до наявності двох груп похибок: систематичних і випадкових.
Систематичні похибки - це похибки, величина яких однакова у всіх вимірах, що проводяться тими ж методами і приладами. Систематичні помилки легко виявити при невеликому числі перевірок за допомогою відомого значення вимірюваної величини. Їх можна усунути, наприклад, калібруванням вимірювального засобу.
Випадкові похибки характеризуються тим, що їх значення різному навіть для вимірювань, виконаних в однакових умовах. До випадкових похибок, наприклад, можна віднести округлення частки поділки приладу експериментатором, який виконує вимір.
З метою обліку випадкових похибок визначається помилка відтворюваності дослідів, яка в залежності від наявних експериментатором ресурсів може бути оцінена різними шляхами:
1. Шляхом постановки паралельних (дублюючих) дослідів в однакових умовах n раз.
2. Нерівномірним дублюванням дослідів в різних точках плану.
3. Проведенням по одному досвіду в кожній точці плану експерименту і проведенням дослідів-дублів в центрі плану при нульових значеннях всіх факторів. При цьому передбачається, що випадкова похибка проведення дослідів і, відповідно, дисперсія визначення величини yi однакова в усьому факторном просторі.
Наприклад, при рівномірному дублювання дослідів середнє значення заміряли параметра одно
де уi-значення параметра в i -тому досвіді,
n - число дослідів паралельних дослідів (дублів).
Дисперсія відтворюваності випадкової величини визначається виразом
де - середньоквадратичне відхилення випадкової величини.
Паралельні досліди повинні бути проаналізовані на наявність грубих помилок. Для виключення помилкових дослідів використовуються спеціальні методи математичної статистики. У першому наближенні при паралельних випробуваннях можна вважати помилковими результати, що виходять за межі двох среднеквадратических відхилень
Якщо число експериментальних точок в плані експерименту одно N і в кожної проводиться по n паралельних дослідів, то дисперсія параметра визначається за формулою
Такий похід до визначення дисперсії відтворюваності справедливий, якщо виконується умова однорідності дисперсій в кожній j-тої точки плану експерімента.Задача перевірки однорідності дисперсій відноситься до завдань статистичної перевірки гіпотез. Загальна схема рішення таких задач полягає в наступному.
1. Вибирається критерій перевірки гіпотези - функція випадкових аргументів з відомим законом розподілу. Це можуть бути критерії Фішера F. Кохрена G або інші.
2. Вибирається рівень значимості критерію - ймовірність того, щоб прийняти вірну гіпотезу невірною. Зазвичай рівень значущості приймається 1%, 2% або 5% (= 0,01; 0,02; 0,05) .З збільшенням величини зростає ймовірність помилки. У техніці часто приймається рівним 0,05.
3. За допомогою таблиць розподілу критерію знаходиться область допустимих значень (граничне значення обраного критерію).
4. За досвідченим даними обчислюється значення критерію і порівнюється з граничним значення обраного критерію. Якщо знайдене значення критерію, знайденого за дослідними даними менше граничного, то гіпотеза приймається, в іншому випадку гіпотеза вважається неправильною.
Для перевірки гіпотези про однорідність двох дисперсій використовується критерій Фішера F, який являє собою відношення максимальної дисперсії до мінімальної для відповідних чисел ступенів свободи і рівнів значущості (див. Додаток 2)
Якщо отримане розрахунком за результатами випробувань значення критерію Фішера F менше табличного значення Fт. то дві дисперсії однорідні.
Розподіл критерію Фішера залежить від двох ступенів свободи:
- для n1 паралельних дослідів, в яких дисперсія виявилася максимальною, і - для n2 паралельних дослідів, в яких дисперсія виявилася мінімальною.
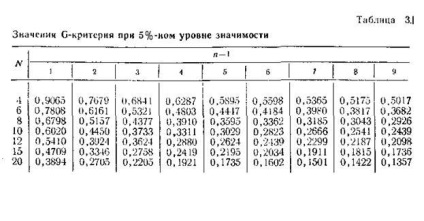
При рівномірному дублювання дослідів (однакове число дослідів в кожній точці плану експерименту) однорідність дисперсій перевіряється за допомогою критерію Кохрена G. який визначається як відношення максимальної дисперсії до суми всіх інших дисперсій
Дисперсії однорідні, якщо розрахункове значення критерію Кохрена Gp
не перевищує табличне значення критерію Gт. Значення Gт наведені в табл. 3.1.