помилки математиків

Саме британський майстер головоломок Генрі Ернест Дьюдени (а математиком він був кращим у порівнянні з Ллойдом) виправив рішення Ллойда. Відомо, що прямокутник можна за допомогою розрізу «сходинками» перетворити в квадрат. Але подібний підхід «працює», тільки коли сторони прямокутника знаходяться в певному співвідношенні, і в даному випадку співвідношення (три до чотирьох) не дозволяє це зробити. Дотепне рішення Ллойда дає квадрат, але довгастий. Дьюдени запропонував правильні рішення з п'ятьма частинами (див. Другий малюнок).

помилки математиків
Іноді знаходять помилки і у тих, хто сам активно спростовує інших. Англієць Анджело Льюїс, який писав книги по головоломок під псевдонімом «Професор Хоффман», привів ось таку головоломку з 20 точками в своїй книзі Puzzles Old and New ( «Старі та нові головоломки») 1893 року.
помилки математиків
Дивлячись на хрест з точок, визначте, скільки різних квадратів можна знайти в різних поєднаннях з чотирьох точок. Хоффман стверджує, що 17. У своїй статті The Best Puzzles with Coins ( «Кращі головоломки з монетами») в журналі The Strand Magazine, Дьюдени доповнив його рішення і привів список з 19 квадратів. Насправді квадратів 21.

Дьюдени привів правильне значення, коли перевидав головоломку в одній зі своїх книг. Читачеві не важко буде знайти 21 квадрат. Однак друга частина головоломки складніша - видаліть 6 точок так, щоб не можна було знайти жодного квадрата взагалі.

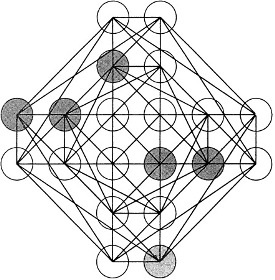
Відповідь: На нижньому малюнку показано сірим кольором, як видалити шість точок, щоб разом знищити 21 сховався квадрат. Рішення унікально, але можливі повороти і відображення.

Матеріали по темі:

Поділитися з друзями:

Схожі статті