Теплоемкостьсістеми (або тіла) - це відношення кількості повідомленої системі теплоти до спостережуваного при цьому підвищення температури (при відсутності хімічної реакції, переходів речовини з одного агрегатного стану в інше).
Теплоємність пропорційна кількості речовини. Розрізняють питому і молярну теплоємність.
Питома теплоємність Суд - це кількість теплоти, необхідне для нагрівання одиниці маси речовини на 1 К. Одиниця виміру питомої теплоємності - Дж / (г × К).
Молярна теплоємність С - це кількість теплоти, необхідне для нагрівання 1 моль речовини на 1 К. Одиниця виміру молярної теплоємності - Дж / (моль × К).
Молярна і питома теплоємності пов'язані співвідношенням:
,
де М - молярна маса.
Розрізняють середню і справжню теплоємності.
Середня теплоємність визначається відношенням повідомленої системі теплоти до спостережуваного при цьому підвищення температури:
Справжня теплоємність С відповідає нескінченно малому зміни температури:
Легко встановити зв'язок між середньою і істинної теплоємності, інтегруючи (1.8) в інтервалі температур від Т1 до Т2 і підставляючи отриманий вираз для Q в (1.7):
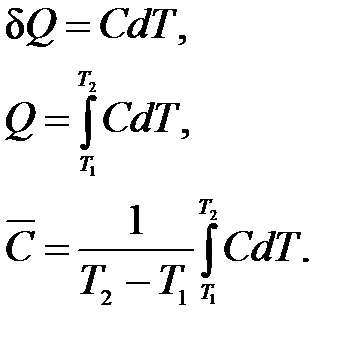
Залежно від умов, при яких виробляється нагрівання, розрізняють теплоємність при постійному обсязі СV (ізохорно теплоємність) і теплоємність при постійному тиску Cp (ізобарну теплоємність):
Якщо нагрівання здійснюється за V = const. вся теплота йде на збільшення внутрішньої енергії; при p = const крім збільшення внутрішньої енергії відбувається робота розширення.
Якщо сталість обсягу або тиску обмовляється, приватну похідну в (1.9) замінюють повною:
Інтегруючи вираження (1.10) в інтервалі температур від Т1 до Т2. і приймаючи, що Cp і СV в зазначеному інтервалі температур постійні, отримаємо:
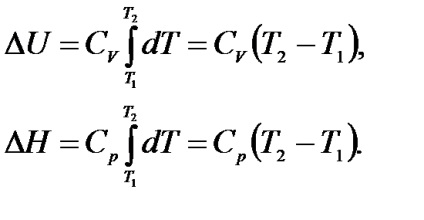
Встановимо взаємозв'язок між Cp і СV для 1 моль ідеального газу. Відповідно до рівняння Менделєєва-Клапейрона (1.1)
.
Ізобарна і ізохорно теплоємності ідеального газу відрізняються на величину універсальної газової постійної R.
Для одноатомного ідеального газу
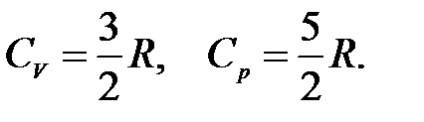
Для двухатомного ідеального газу при середніх температурах
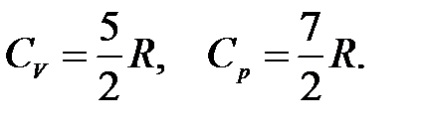
Ізобарна і ізохорно теплоємності твердих речовин практично рівні.
Теплоємність твердих, рідких і газоподібних тіл залежить від температури. Найбільш часто залежність теплоємності індивідуальних речовин від температури виражається емпіричним рівнянням виду:
де a. b. c. c '- емпіричні коефіцієнти, обчислені на основі експериментальних даних.
Для органічних речовин коефіцієнт c '= 0, для неорганічних - c = 0.
Дане емпіричне рівняння може бути застосовано тільки в певному інтервалі температур. Тому коефіцієнти a, b, c і c 'не мають фізичного сенсу. Для багатьох речовин вони наведені в довідниках (із зазначенням температурного інтервалу, в якому їх можна використовувати).
1.3.3 Вплив температури на тепловий ефект
хімічної реакції. рівняння Кірхгофа
Температура дуже впливає на теплові ефекти хімічних реакцій. Поставимо задачу кількісно охарактеризувати цей вплив.
Розглянемо хімічну реакцію, що протікає при р = const:
.
Нехай ентальпія вихідних речовин, що беруть участь в реакції дорівнює Н1. а ентальпія продуктів реакції - Н2. тоді
де - теплоємність системи в початковому стані:
.
Аналогічно, для продуктів реакції:
.
Віднімаючи почленно з рівняння (1.13) рівняння (1.12), отримаємо:
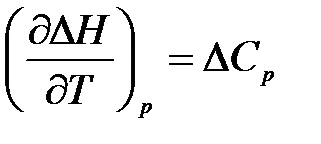
Для хімічної реакції одно
.
Аналогічно для процесів, що протікають при V = const,
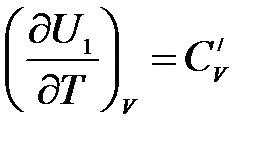
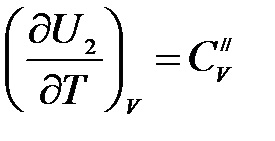
Для хімічної реакції
.
Отримані рівняння (1.13), (1.14) виражають закон Кірхгофа:
Температурний коефіцієнт теплого ефекту хімічної реакції (або інших процесів), що протікають при р = const або V = const дорівнює різниці теплоємностей системи в початковому і кінцевому стані.
Проаналізуємо рівняння Кірхгофа.
З рівнянь випливає, що вплив температури на тепловий ефект обумовлюється знаком величини:
- якщо # 916; Ср> 0, то похідна
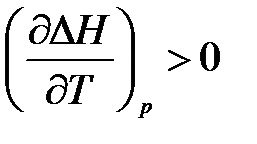
- якщо # 916; Ср <0, то производная
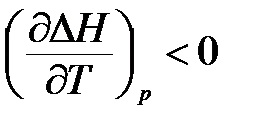
- якщо # 916; Ср = 0, то тепловий ефект реакції не залежить від температури.
Закон Кірхгофа дозволяє розраховувати теплові ефекти реакції при будь-якій температурі.
Отримаємо рівняння для розрахунку теплового ефекту, що протікає при
р = const. Розділимо змінні в рівнянні Кірхгофа:
.
При інтегруванні рівняння Кірхгофа часто використовується температурна залежність теплоємності в вигляді статечних рядів, які справедливі у певному температурному інтервалі. Найчастіше інтегрування проводять в певних межах, прийнявши за нижню межу інтегрування температуру 298 К, а за верхній - температуру Т. Тепловий ефект реакції при 298 К можна легко розрахувати, використовуючи перше або друге слідства із закону Гесса. В результаті інтегрування отримаємо:
Так як ізобарна теплоємність має властивості функції стану, для # 916; Ср можна записати:
,
,
,
,
.
Підставивши вираз для # 916; Ср в (1.15) і проинтегрировав, отримаємо:
.
Якщо в інтервалі температур від 298 К до Т одне з реагуючих речовин зазнає зміна агрегатного стану, тобто відбувається фазовий перетворення, то інтервал температур розбивається на два інтервали: від 298 К до Тф.п. (Температура, при якій відбувається фазовий перехід) і від Тф.п. до Т:
.
Обчислення теплового ефекту за рівнянням Кірхгофа значно спрощується, якщо скористатися середніми теплоємності для реагентів або прийняти, що не залежить від температури в даному інтервалі.
Наведемо рівняння (1.16) до виду
.
Вираз, укладену в дужки, завжди постійно, таким чином, в даному випадку залежність теплового ефекту від температури є лінійною. Недолік даного методу розрахунку теплових ефектів полягає в його невисокої точності.