Другий чудовий межа
Перший чудовий межа
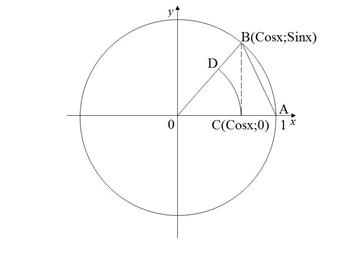
Доведення. Покажемо спочатку, що при. Так як всі функції, що входять в нерівність, парні, то розглянемо випадок.
Очевидно, площа криволінійного сектора OCD менше площі трикутника OAB, а вона менша за площу криволінійного сектора OAB. Скористаємося формулою площі криволінійного сектора: (r - радіус, х - центральний кут). тоді
Розділимо всі частини останнього нерівності на х і помножимо на два, одержимо. Переходячи до межі при у всіх годину-тях останнього нерівності, отримаємо, що й треба було довести. # 9632;
Зробивши в останньому межі заміну, отримаємо
Затвердження Якщо і, то
В останньому прикладі при отримаємо.
а) Еквівалентні функції.
Відповідь: Якщо в деякій проколеної околиці точки функція подана в вигляді, причому, то функції і називають еквівалентними при і пишуть
Затвердження Якщо і в деякій, то
при тоді, і тільки тоді, коли.
Наприклад, при, так як; , так як .
Таблиця еквівалентних функцій при
Теорема Якщо і при, то
б) Поняття нескінченно малої функції в порівнянні з іншого.
Відповідь: Якщо в деякій проколеної околиці точки функція подана в вигляді, причому, то функцію називають нескінченно малою в порівнянні з при і пишуть,.
Затвердження Якщо в деякій, то при тоді, і тільки тоді, коли.
Приклад 1) при; 2) при.
Якщо і - обидві нескінченно малі при, то кажуть, що є нескінченно мала вищого порядку, ніж при.
Деякі важливі властивості символу.
Доведемо, наприклад, що. Дійсно,, так як якщо і нескінченно малі, то теж нескінченно мала # 9632;
4 Безперервні функції