Функції є нескінченно малими, якщо при прагненні x до точки а їх межа дорівнює 0.
Однак нескінченно малої функція може бути тільки в конкретній точці. Як показано на малюнку 1, функція нескінченно мала тільки в точці 0.
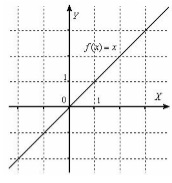
Малюнок 1. Нескінченно мала функція
Якщо межа приватного двох функцій в результаті дає 1, функції називаються еквівалентними нескінченно малими при прагненні х до точки а.
Якщо функції f (x), g (x) нескінченно малі при $ х> а $, то:
- Функція f (x) називається нескінченно малою вищого порядку щодо g (x), якщо виконується умова: \ [\ mathop \ limits_ \ frac = 0 \]
- Функція f (x) називається нескінченно малою n-го порядку щодо g (x), якщо відмінний від 0 і кінцевий межа: \ [\ mathop \ limits_ \ frac (x)> = A \]
Функція $ y = х ^ 3 $ є нескінченно малою вищого порядку при х> 0, в порівнянні з функцією y = 5x, так як межа їх відносини дорівнює 0, це пояснюється тим, що функція $ y = х ^ 3 $ прагне до нульового значенням швидше:
Функції y = x2-4 і y = x2-5x + 6 є нескінченно малими одного порядку при х> 2, так як межа їхні стосунки не дорівнює 0:
Властивості еквівалентних нескінченно малих
- Різниця двох еквівалентних нескінченно малих є нескінченно мала вищого порядку щодо кожної з них.
- Якщо з суми кількох нескінченно малих різних порядків відкинути нескінченно малі вищих порядків, то решта, звана головною, еквівалентна всій сумі.
З першого властивості слід, що еквівалентні нескінченно малі можуть стати наближено рівними зі як завгодно малої відносної похибкою. Тому знак ≈ застосовується як для позначення еквівалентності нескінченно малих, так і для запису наближеного рівності їх досить малих значень.
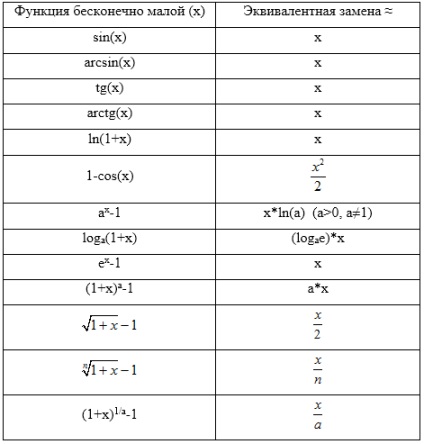
При знаходженні меж дуже часто доводиться застосовувати заміну еквівалентних функцій для швидкості і зручності обчислень. Таблиця еквівалентних нескінченно малих представлена нижче (табл.1).
Еквівалентність нескінченно малих наведених в таблиці можна довести, спираючись на рівність:
Заміна еквівалентних величин