Пустьy- деяка функція переменнойx; причому, неважливо, яким чином ця функція задана: формулою, таблицею або якось інакше. Важливий тільки сам факт існування цієї функціональної залежності, що записується в такий спосіб: y = f (x). Букваf (початкова буква латинського слова "functio" - функція) не позначав будь-якої величини, так само як буквиlog, sin, tanв записах функційy = logx, y = sinx, y = tanx.Оні говорять лише про певні функціональних завісімостяхyотx. Запісьy = f (x) представляетлюбуюфункціональную залежність. Якщо дві функціональні залежності: yотxіzотtотлічаются одна від одної, то вони записуються за допомогою різних букв: y = f (x) іz = F (t). Якщо ж деякі залежності одні й ті ж, то вони записуються однією і тією ж буквойf: y = f (x) іz = f (t). Якщо вираз для функціональної завісімостіy = f (x) відомо, то вона може бути записана з використанням обох позначень функції. Наприклад, y = sin x або f (x) = sin x. Обидві форми повністю рівносильні. Іноді використовується і інша форма запису: y (x). Це означає те ж саме, що і y = f (x).
Графічне представлення функцій.
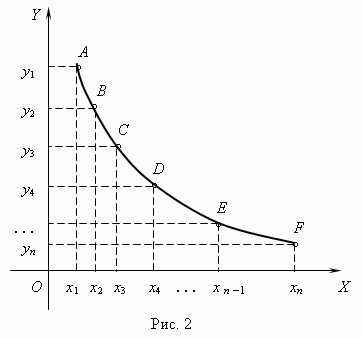
Щоб уявити функціюy = f (x) у вигляді графіка, потрібно:
1) Записати ряд значень функції і її аргументу в таблицю:
2) Перенести координати точок функції з таблиці в систему координат,
відзначивши відповідно до обраним масштабом значення абсцис на
осіХі значення ординат на осіY (рис.2). В результаті в нашій системі
координат буде побудований ряд точекA, B, C. F.
3) Поєднуючи точкіA, B, C. Fплавной кривої, отримуємо графік заданої
Таке графічне представлення функції дає наочне уявлення про характер її поведінки, але досягається при цьому точність недостатня. Можливо, що проміжні точки, не збудовані на графіку, лежать далеко від проведеної плавною кривою. Хороші результати в значній мірі залежать також від вдалого вибору масштабів. Тому слід определітьграфік функції какгеометріческое місце точок, коордінатикоторих M (x, y) пов'язані заданої функціональної залежністю.
Область визначення і область значень функції. У елементарної математики вивчаються функції тільки на множині дійсних чисел R. Це означає, що аргумент функції може приймати тільки ті дійсні значення, при яких функція визначена, т.e. вона також приймає тільки дійсні значення. Безліч X всіх допустимих дійсних значень аргументу x. при яких функція y = f (x) визначена, називається областю визначення функції. Безліч Y всіх дійсних значень y. які приймає функція, називається областю значень функції. Тепер можна дати більш точне визначення функції: правило (закон) відповідності між множинами X і Y. за яким для кожного елемента з безлічі X можна знайти один і тільки один елемент з безлічі Y, називається функцією.