б) кожен набір проміжних вершин, що лежать уздовж неудліняемих ділянок шляху з нульовою довжиною, визначає одну операцію. Такими наборами в наведеному прикладі будуть;
в) кожна проміжна дуга довжиною в один символ визначає зміну верстата. Отже, довжина шляху без одиниці дорівнює числу операцій.
З цих властивостей випливає зведення, оскільки по найкоротшому шляху з витоку в стік на побудованому зваженому орграфе однозначно знаходиться розбиття послідовності переходів на мінімальне число операцій [22].
На рис. 2.14 горизонтальні дуги навантажені нулем, інші - одиницею; жирні дуги позначають найкоротший шлях, відповідний рішенням (б) на рис. 2.13; довжина шляху без одиниці дорівнює числу операцій, т е. трьом операціям:
· Операція включає переходи і виконується на верстаті;
· Операція включає перехід і виконується на верстаті;
· Операція включає переходи і виконується на верстаті.
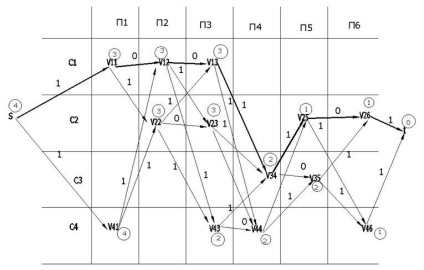
Мал. 2.14 Приклад формування технологічних операцій як пошуку Найкоротшого Шляхи на орграфе
2.2.7 Балансування технологічного маршруту
Наступна виробнича задача, зводиться до задачі пошуку шляху на графі, виникає при виборі технологічних маршрутів обробки деталей в гнучкою виробничої системи (ГВС).
Нехай на вхід деякої ДПС надійшла партія однакових деталей для виготовлення виробів однієї номенклатури. Задана встановлена для цієї номенклатури послідовність технологічних операцій. Для кожної операції визначені допустимі призначення на верстати ГПС і час її виконання кожним відповідним верстатом. Час виконання операції може залежати від верстата, який її виконує. Відомо час транспортування деталі від одного верстата до іншого. Потрібно так призначити операції на верстати, щоб одержуваний при цьому технологічний маршрут проходження верстатів був збалансований (т. Е. Тривалості обробки і транспортування деталі на всіх ділянках маршруту, по можливості, вирівняні). Балансування технологічного маршруту призводить до найбільш рівномірного завантаження устаткування ГВС [22].
Нехай - послідовність операцій, а - верстати ДПС. Побудуємо орграф з вершинами s, t і вершинами для кожної операції і кожного верстата, який може її виконати. Вершини з'єднаємо дугами для всіх допустимих наборів значень i, j, k.
Всі дуги виду навантажимо часом виконання операції станком, все дуги виду, - часом транспортування від верстата; до верстата, а все дуги виду - нулем.
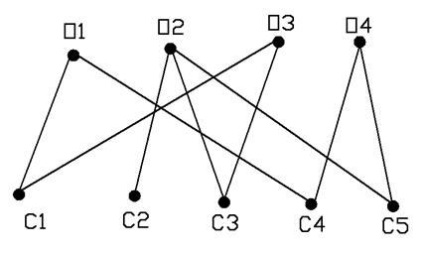
Мал. 2.15 Приклад допустимих призначень операцій на верстати
Розглянемо приклад побудови орграфа при п = 4, т = 5. Допустимі призначення операцій на верстати визначені ребрами двудольного графа на рис. 2.15, а час виконання операцій відповідними верстатами і час транспортування представлені в таблицях 2.9 і 2.10. Клітини, що відповідають неприпустимим призначень операції на верстати, що не заповнені. На рис. 2.16 зображений відповідний орграф.
Довільний шлях на побудованому орграфе з s в t проходить через проміжні вершини і має такі властивості:
а) він визначає варіант допустимого призначення операцій на верстати, оскільки - це номери верстатів, які повинні виконувати операції. Причому немає жодного варіанту допустимого призначення операцій, якому не відповідав би певний шлях з s в t.
б) відповідний шлях маршрут проходить верстати в послідовності. Найдовша дуга шляху визначає найтриваліший за часом процес на маршруті. Якщо такий дугою виявиться, то самим тривалим процесом буде операція, якщо то - транспортування від верстата до верстата
Збалансованому маршруту поставимо у відповідність шлях з s в t з найбільш короткою найдовшого дугою. Тим самим час найбільш тривалого процесу на маршруті ми зробимо по можливості менше і наблизимо його до часу інших. Така інтерпретація критерію балансування остаточно зводить вихідну задачу до задачі найтонші ШЛЯХ [22].