Ми бачимо, що, хоча приклади 1 і 2 дуже різні, їх рішення абсолютно однакові. Засновані вони на загальному правилі множення.
Для того щоб знайти число нд ?? ех можливих результатів незалежного проведення двох випробувань А і В. слід перемножити число нд ?? ех результатів випробування А і число нд ?? ех результатів випробування В.
Правило множення для двох незалежних випробувань зручно пояснювати, використовуючи прямокутники, розбиті на квадратики, або прямокутні таблиці. Але якщо проводяться три випробування, то для ілюстрації потрібно використовувати і довжину, і ширину, і висоту, і на зображенні вийде прямокутний паралелі ?? епіпед, розбитий на кубики. Тут уже малюнок і пояснення стають складніше, оскільки, наприклад, будуть невидимі кубики. Ще гірша справа з чотирма випробуваннями. В цьому випадку для малюнка нам просто не вистачить вимірювань, адже навколишній нас простір нд ?? його лише трехмерно.
Виявляється, правило множення для трьох, чотирьох і т. Д. Випробувань можна пояснити, не виходячи за рамки площині, за допомогою геометричної моделі, яку називають деревом можливих варіантів. Вона, по-перше, наочна як будь-яка картинка, і, по-друге, дозволяє вс ?? е врахувати, нічого не пропустив.
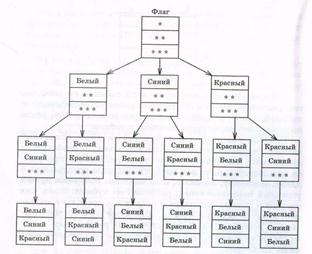
Рішення. Будемо шукати рішення за допомогою дерева можливих варіантів (рис. 4.1). Подивимося на його ліву''веточку'', що йде від''флага'', нехай верхня смуга - білого цвета͵ тоді середня смуга повинна бути син ?? їй або червоною, а нижня - відповідно, червоною або син ?? їй. Вийшло два варіанти кольорів смуг прапора: біла, синя, червона і біла, червона, синя.
Нехай тепер верхня смуга - син ?? його цвета͵ це друга''веточка''.
Тоді середня смуга повинна бути білою або червоною, а нижня - відповідно, червоною або білою. Вийшло ще два варіанти кольорів смуг: синя, біла, червона і синя, червона, біла.
Аналогічно розглядається випадок для верхньої смуги червоного кольору. Вийде ще два варіанти: червона, біла, синя і червона, синя, біла смуги прапорів. Всього 6 комбінацій.
Побудована схема дійсно нагадує дерево, тільки перевернуте. Мабуть, у зв'язку з цим її і називають деревом можливих варіантів.
Ось як, наприклад, виглядає дерево можливих варіантів для прикладу 1 (рисунок 4.2):
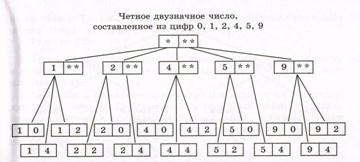
Приклад 4. У коридорі висять три лампочки. Скільки є різних способів освітлення коридору?
Перший спосіб. Пронумеруємо лампочки і будемо писати'' +'' або''-'' виходячи з того, горить або не горить чергова лампочка. Тоді нд ?? е способи освітлення можна просто перерахувати: + + +, + + -, + - +, - + +, + - -, - + -, - - +,
Всього 8 способів.
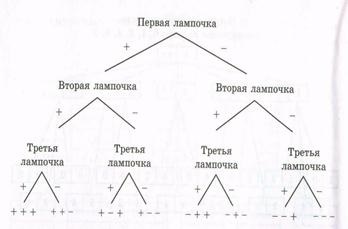
Третій спосіб. Перша лампочка може або горіти, або НЕ горіти, ᴛ.ᴇ. є два можливих результату. Те ж саме відноситься і до другої, і до третьої лампочкам. Ми припускаємо, що лампочки горять чи ні незалежно один від одного. за
Малюнок 4.3 правилом множення отримуємо, що число нд ?? ех способів освітлення дорівнює 2 ‣‣‣ 2 ‣‣‣ 2 = 8.
У кожного з цих трьох способів вирішення в кожному конкретному випадку є свої переваги і свої недоліки. Вибір способу вирішення - за вами! Відзначимо нд ?? е ж, що правило множення дозволяє в один крок вирішувати найрізноманітніші завдання. Наприклад, воно призводить до вкрай важливого в математиці поняттю факторіала. Розглянемо спочатку приклади.
Приклад 5. У сім'ї - 6 осіб, і за столом в кухні стоять 6 стільців. У родині вирішили щовечора, вечеряючи, сідати на ці 6 стільців по-новому. Скільки днів члени сім'ї зможуть робити це без повторень?
Рішення. Відповідь виявляється несподівано великим: майже два роки! Пояснимо його. Для зручності міркувань будемо вважати, що сім'я (бабуся, дідусь, мама, тато, дочка, син) буде сідати на стільці по черзі. Нас цікавить, скільки нд ?? його існує різних способів їх розміщення на стільцях.
Припустимо, що першою вмощується бабуся. У неї є 6 варіантів вибору стільця. Другим сідає дідусь і незалежно обирає стілець з 5 залишилися. Мама робить свій вибір третьої і вибір у неї буде з 4 стільців. У тата буде вже 3 варіанта͵ у дочки - 2, ну а син сяде на єдиний незайнятий стілець. За правилом множення отримуємо, що вс ?? його є 6 · 5 · 4 · 3 · 2 · 1 = 720 різних способів розміщення. Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, в''ігру з рассажіваніямі'' сім'я може грати 720 днів, т. Е. Майже 2 роки.
Приклад 6. Десять різних листів розкладають по одному в десять конвертів. Скільки існує способів такого розкладання?
Рішення. Запропонована ситуація відрізняється від попередньої (приклад 5). Дійсно, там були люди і стільці, тут - листи і конверти. При цьому і тут, і там потрібно дізнатися, скількома способами можна розмістити п предметів на п місцях.
Повторюючи попереднє рішення, отримуємо, що вс ?? його є 10 · 9 · 8 · 7 · 6 · 5 · 4 · 3 · 2 · 1 = 3 628 800 способів розкладання листів у конверти. Понад 3,5 мільйонів!
Як ми бачимо, умови задач - різні, а рішення, та й отримані відповіді, по суті справи, однакові. Зручно в зв'язку з цим ввести і однакові позначення для таких відповідей.
Визнач ?? еніе.Проізведеніе перших поспіль п натуральних чисел позначають п!
Знак п! читається як''ен факторіал'', що в дослівному перекладі з англійської мови означає''состоящій з п множник ?? ей''. Наведемо кілька перших значень для п:
6! = 1 · 2 · 3 · 4 · 5 · 6 = 720 і т.д.
Розглянемо ще кілька прикладів:
Рішення. а) 3! = 1 # 8729; 2 # 8729; 3 = 6.
б) тому що 7! = 1 # 8729; 2 # 8729; 3 # 8729; 4 # 8729; 5 # 8729; 6 # 8729; 7 і 5! = 1 # 8729; 2 # 8729; 3 # 8729; 4 # 8729; 5, то 5! можна винести за дужки, тоді отримаємо 5! (6 # 8729; 7-1) = 1 # 8729; 2 # 8729; 3 # 8729; 4 # 8729; 5 # 8729; 41 = 4920.
Приклад 8. Спростити вираз:.
Рішення. = 1 # 8729; 2 # 8729; 3 # 8729; ... # 8729; (п-1) # 8729; п # 8729; (п + 1), а = 1 # 8729; 2 # 8729; 3 # 8729; ... # 8729; (п-1), після скорочення отримаємо п # 8729; (п + 1).
Як же сформулювати загальне твердження, окремими випадками якого є рішення прикладів 3, 5 і 6? Ось один з можливих варіантів.
ТЕОРЕМА: п різних елементів можна привласнити номери від 1 до п рівно п! різними способами.
Кожен спосіб нумерації від 1 до п. Про який йде мова в теоремі, часто називають перестановкою даного п -елементного безлічі. Дійсно, можна вважати, що кожна така нумерація просто розставляє або переставляє нд ?? е елементи безлічі в деякому порядку.
Перестановками з п елементів називають комбінації, які відрізняються один від одного тільки порядком елементів.
Число перестановок безлічі з п елементів позначають Рп. Значить, наведену теорему можна записати у вигляді формули:
Крім правила множення в комбінаториці іноді використовується ще правило складання: Для того щоб знайти число нд ?? ех можливих результатів незалежного проведення одного з двох випробувань А чи В, слід скласти число нд ?? ех результатів випробування А і число нд ?? ех результатів випробування В.
Приклад 9. На столі в стаканчику коштує 5 олівців і 3 ручки. Для того, щоб написати записку (записати тел ?? Ефона номер і т.п.), ми можемо взяти 1 з 5 олівців або 1 з 3 ручок, тобто у нас є 5 можливостей вибору одного олівця і 3 можливості вибору однієї ручки. Так як ми вибираємо тільки 1 предмет, олівець або ручку, то число нд ?? ех можливостей вибору одно: 5 + 3 = 8.
Правила множення і складання застосовні для будь-якої кількості незалежних випробувань.
Підіб'ємо підсумки нашого знайомства з найпростішими комбінаторними завданнями. Ми отримали основне правило - правило множення, розглянули його геометричну модель - дерево можливих варіантів, ввели нове поняття - факторіал, сформулювали теорему про перестановки, в якій це поняття використовується.