2 Глава 1.Разложеніе вектора по двом неколінеарна векторах. Лемма про колінеарних векторах.Лемма про колінеарних векторах. Якщо вектори а і в Колінеарні і а = 0, то існує таке число R, що в = Rа.Еслі вектори а і в Колінеарні і а = 0, то існує таке число R, що в = R. Доказ: доказ: для доказу, можливі два випадки. для доказу, можливі два випадки. 1 а в. Візьмемо число R = | в | | А |. Так як R0, то вектори R а і в сонаправлени (рис.1). Крім того, їх довжини рівні: | R а | = | R | · | а | = | у | | А | · | а | = | у | .Тому в = R. 2 а в. Візьмемо число R = - | в | | А |. Так як R0, то вектора R а і в знову сонаправлени. (Рис2). Їх довжини є рівними: | R а | = | R | · | а | = | у | | А | · | а | = | у |. Тому в = R Лема доведена. Ріс.1Ріс.2 а в а а в а R R R = | в | / | а | R = - | в | / | а |

3 Теорема: будь-який вектор можна розкласти по двом даними неколінеарна векторах, причому коефіцієнти розкладання визначаються єдиним чином. Доказ: Нехай a і b-дані неколінеарна вектора. Доведемо спочатку, що будь-який вектор p можна розкласти по векторах a і b. Можливі два випадки. Але ми з вами розглянемо перший випадок. Вектор p коллінеарен одному з векторів a і b, наприклад вектору b. В цьому випадку по лемі про колінеарних векторах вектор p можна представити у вигляді p = y · b, де y-деяке число, і, отже, p = 0 · a + y · b, тобто. вектор p розкладений по векторах a і b. a b c

4 Поняття прямокутної системи координат нам відомо з курсу алгебри. нагадаємо, що для завдання прямокутної системи координат потрібно провести дві взаємно перпендикулярні прямі, на кожній з них вибрати напрямок (воно позначається стрілкою) і вибрати одиницю виміру відрізків. При обраному об'єкті вимірювання відрізків довжина кожного відрізка виражається позитивним числом. Надалі під довжиною відрізка ми будемо розуміти це число. Відкладемо від початку координат Про одиничні вектори (тобто. Вектора, довжини яких дорівнюють одиниці) i і j так, щоб напрямок вектора i співпало з напрямком осі Ox, а напрямок вектора j- з напрямком осі Oy (рис.1). Вектора i і j назвемо координатами вектора. Координатні вектора НЕ колінеарні, тому будь-який вектор p можна розкласти по координатним векторах, тобто представити у вигляді p = xi + yj, причому коефіцієнти розкладання (числа х і у) визначаються єдиним чином. Коефіцієнти розкладання вектора p по координатним векторах називаються координатами вектора p в даній системі координат. Координати вектора будемо записувати в фігурних дужках після позначення вектора: p. На малюнку (рис.1) OA, b. Так, як нульовий вектор можна представити у вигляді 0 = 0 · i + 0 · j, то його координати дорівнюють нулю: 0. Якщо вектори a = x 1 i + y 1 j і b = x 2 i + y 2 j рівні, то х 1 = х 2 і у 1 = у 2. таким чином, координати рівних векторів відповідно рівні. х у j i А Про У З -2j 3i3i b

5 Найголовніше вам треба запам'ятати правила, що дозволяють за координатами векторів знаходити координати їх суми, різниці та добутку векторів на число. 1! Кожна координата суми двох або більше векторів дорівнює сумі відповідних координат цих векторів. (A + b рівні). 2! Кожна координата різниці двох векторів дорівнює різниці відповідних координат цих векторів. (A-b рівні). 3! Кожна координата добутку вектора на число дорівнює добутку відповідної координати вектора на це число. (Тобто.)

6 Завдання 1. 3a-xb = ya + b; y = 3, x = -1. Завдання 2. 4a-xa + 5b + yb = 0; 4a + 5b = xa-yb; x = 4, y = -5.
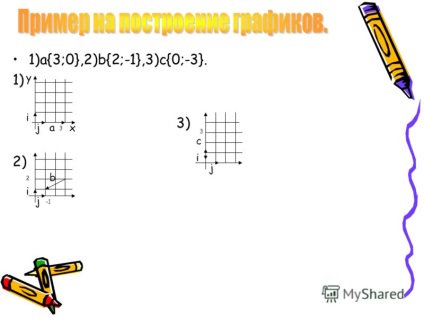
7 1) a, 2) b, 3) c. 1) 2) i jax y b j i 3) c 3 i j 2 3