Презентація на тему: "Рішення раціональних нерівностей методом інтервалів Мета: вирішуючи нерівності методом інтервалів, розглянути особливі випадки - коріння парному кратності і точки." - Транскрипт:
1 Рішення раціональних нерівностей методом інтервалів Мета: вирішуючи нерівності методом інтервалів, розглянути особливі випадки - коріння парному кратності і точки розриву. Визначення: Раціональними називають нерівності, що містять тільки цілі раціональні або дрібно - раціональні функції.

2 Метод інтервалів полягає в наступному: Числова пряма розбивається нулями функції на кінцеве число інтервалів, на кожному з яких функція зберігає знак.

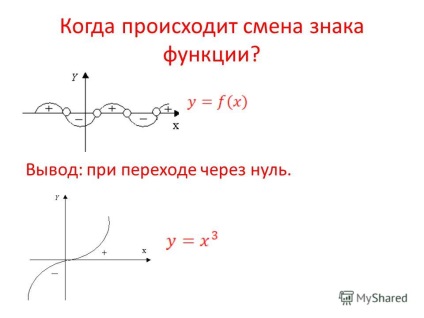
3 Коли відбувається зміна знака функції? Висновок: при переході через нуль.
5 Усно Рішень немає Висновок: вираз, що стоїть в парному ступеня, не впливає на знак нерівності, але впливає на рішення і відкидати його без додаткових обмежень не можна

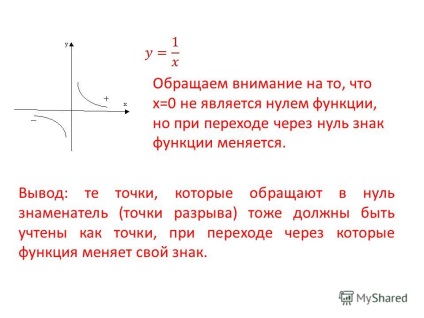
6 Звертаємо увагу на те, що х = 0 не є нулем функції, але при переході через нуль знак функції змінюється. Висновок: ті точки, які звертають в нуль знаменник (точки розриву) теж повинні бути враховані як точки, при переході через які функція змінює свій знак.
7 Розглянемо рішення нерівності: Висновок: х = -2 - корінь парному кратності, при переході через який функція знак не змінює.

9

10
11

12
13 Вирішити нерівності: 77 (в, г) 78 (в, г, е) 80 (а) 81 (в) Будинок: 78 (а, б) 79 (в) 81 (а, б)
