
Умова:
Тіло, обертаючись равноускоренно з кутовим прискоренням ε = 2 рад / с, має в момент часу t1 = 2,5 c кутову швидкість ω1 = 40 рад / с.
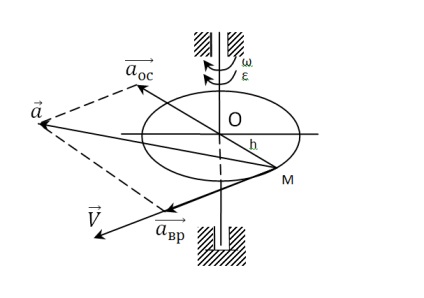
Визначити: 1) швидкість і прискорення точки тіла, що відстоїть на відстані h = 55 см від осі обертання в момент t2 = 7 с; 2) число обертів N тіла за час t3 = 10 c; рівняння обертального руху тіла, якщо в початковий момент часу t0 = 0 початковий кут повороту φ0 = 0.
Рішення:
1. При рівноприскореному обертанні кутова швидкість тіла змінюється за законом
Знаючи значення кутової швидкості ω1 в певний момент часу t1 і кутове прискорення α, можна знайти початкову кутову швидкість ω0 при t0 = 0:
Звідси кутова швидкість тіла в момент часу t2 = 7 з дорівнюватиме
Швидкість V і ускореніеα точки М тіла, віддаленого на відстані h = 55 см від осі обертання, в момент часу t2 = 7 з дорівнюватимуть:
v = ω2 · h = 49 · 55 = 2695 см / с = 26,95 м / с;
αвр = ε · h = 2 · 55 = 110 см / с 2 = 1,10 м / с 2;
αос = ω 2 · h = 49 2 · 55 = 132 055 см / с 2 = 1320,6 м / с 2;
Напрямок векторів швидкості і прискорень дивіться на малюнку до задачі.
Число оборотів тіла за час t3 = 10 c визначимо за співвідношенням
де n (t) - число оборотів тіла за секунду в даний момент часу.
У розглянутій нами задачі
Рівняння обертального руху тіла φ = φ (t) отримаємо зі співвідношення? (T) = dφ / dt => dφ = ω (t) · dt. Інтегруючи даний диференціальне рівняння з урахуванням початкових умов (t0 = 0, φ0 = 0):
Рішення завдання з теоретичної механіки з кінематики завершено.
З повагою, Адміністратор сайту.