Зверніть увагу, на цьому сайті є онлайн-сервіс для обчислення центра ваги і моментів інерції складових перетинів, які складаються з прокатних профілів (двотавр, куточок і т.д.) і з простих фігур.
Часто при розрахунку елементів будівельних конструкцій доводиться визначати геометричні характеристики профілів, складених з елементарних геометричних фігур (прямокутник, коло і т.п.) і прокатних профілів. Розглянемо докладно приклад розрахунку.
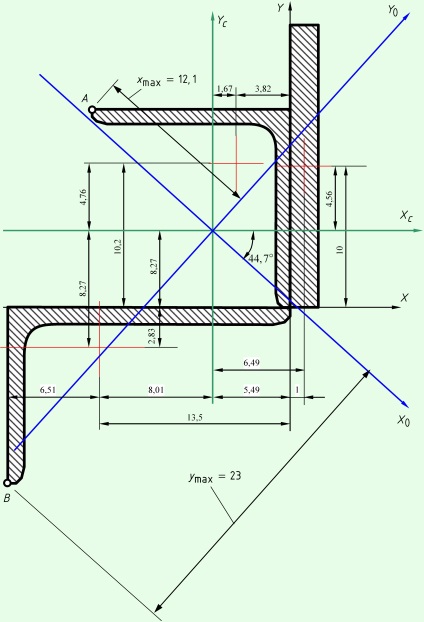
Необхідно визначити геометричні характеристики складеного перерізу (рис.), Який складається з куточка 20 / 12,5 / 1,2, куточка 14/1 і прямокутника 20х2см.
Визначення власних характеристик окремих профілів - складових перетину
Власні характеристики прокатних профілів визначаються з сортаменту.
Для нерівнополочні куточка 20 / 12,5 / 1,2:
- висота і ширина куточка h = 20 см, b = 12,5 см;
- площа $ A $ = 37,9 см 2;
- власні осьові моменти інерції $$ = 1570 см 4. $$ = 482 см 4;
- власний відцентровий момент інерції $> $ = 505 см 4;
- координати центру ваги $$ = 2,83 см, $$ = 6,51 см.
Для рівнополичного куточка 14/1:
- висота і ширина куточка h = b = 14 см;
- площа $ A $ = 27,3 см 2;
- власні осьові моменти інерції $$ = $$ = 512 см 4;
- власний відцентровий момент інерції $> $ = 301 см 4;
- координати центру ваги $$ = $$ = 3,82 см.
Для прямокутника 20х2см:
- висота і ширина прямокутника h = 20 см, b = 2 см;
- площа $ A $ = 20 ∙ 2 = 40 см 2;
- власний відцентровий момент інерції $> $ = 0, так як профіль має вісь симетрії.
Визначення центра ваги перерізу
Загальна площа всього перерізу A = 37,9 + 27,3 + 40 = 105см 2.
Проводимо допоміжні осі $ X $ і $ Y $ і визначаємо щодо них центр ваги перерізу:
При цьому в координатах центрів тяжіння складових обов'язки 'обов'язково враховуємо знак. Відкладаємо осі, які проходять через центр ваги - центральні осі $ Xc $ і $$.
Визначення центральних моментів інерції
Осьові і відцентрові моменти інерції перерізу визначаємо за формулами переходу між паралельними осями. Для цього знаходимо і показуємо на кресленні відстані між центральними осями всього перерізу і власними осями кожної з фігур.
$ = 505 + (- 8,01) \ cdot (- 8,27) \ cdot 37,9 - 301 + 1,67 \ cdot 4,76 \ cdot 27,3 + 0 + 6,49 \ cdot 4,56 \ cdot 40 = 4120 $ см 4.
При цьому обов'язки 'обов'язково враховуємо розміщення фігур щодо розглянутих осей. Так, при визначенні моменту інерції $$ в формулу підставляємо власний момент інерції нерівнополочні куточка щодо осі, яка паралельна осі $$, в сортаменті це вісь $ Y $, і навпаки.
Визначення положення головних осей і головних моментів інерції
Кут повороту головних осей щодо осей, для яких відомі моменти інерції, визначається за формулою
Якщо $ \ alpha> 0 $, головні осі відкладаються проти годинникової стрілки, і навпаки.
Головні моменти інерції визначаються так
$ = 6360 \ cdot (- 44,7 ^ \ circ) + 6280 \ cdot (- 44,7 ^ \ circ) - 4120 \ cdot \ sin (- 2 \ cdot 44,7 ^ \ circ) = 10430 $ см 4 .
$ = 6280 \ cdot (- 44,7 ^ \ circ) + 6360 \ cdot (- 44,7 ^ \ circ) + 4120 \ cdot \ sin (- 2 \ cdot 44,7 ^ \ circ) = 2210 $ см 4 .
Відцентровий момент інерції щодо головних осей дорівнює нулю.
Радіуси інерції. моменти опору
Радіуси інерції перерізу
Моменти опору перерізу визначаємо щодо центральних осей. Для цього необхідно визначити відстані $> $ і $> $ до максимально віддалених точок від головних осей. Спочатку необхідно по кресленнях визначити, які точки є найбільш віддаленими. У нашому випадку це точки $ A $ і $ B $ (рис.). Шукані відстані можна визначити, маючи координати цих точок в центральних (не повернутих осях).
$> = \ Cdot \ cos \ left (\ alpha \ right) + \ cdot \ sin \ left (\ alpha \ right) $
$> = \ Cdot \ cos \ left (\ alpha \ right) - \ cdot \ sin \ left (\ alpha \ right) $
X А = - 8,53см Y A = 8,57см
X B = - 14,5 см Y B = - 18см
x max = - 12,1см y max = - 23см