2. Операторний зображення постійної напруги.
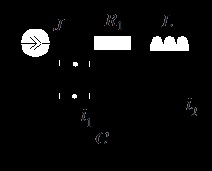
3. Операційна схема заміщення показана на рис. 9.9. Розрахунок операторної схеми виконаємо методом контурних струмів:
Конденсатор на операторної схемою представлений двома елементами. Для розрахунку краще розглянути контур, в рівняння для якого входить зображення (див. Рис. 9.9). тоді отримуємо
.
Розрахувати операційним методом струми в гілках схеми, показаної на рис. 9.9. У схемі діє ідеальне джерело постійного струму А. Параметри елементів: Ф; Гн; Ом.
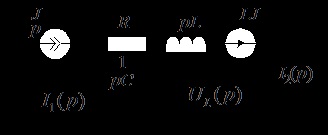
1. Незалежні початкові умови:
2. Операторний зображення задає струму.
3. Операційна схема приведена на рис. 9.11. Її розрахунок виконаємо по рівняннях Кірхгофа:
;
;
Котушка індуктивності представлена її операційним опором і е.р.с початкових умов. Для визначення запишемо рівняння за другим законом Кірхгофа для зазначеного на схемі контуру:
,
Подальший розрахунок виконаємо в цифрах:
;
.
4. Перехід до оригіналів виконаємо по теоремі розкладання. Для вибору модифікації теореми розкладання визначимо коріння многочлена знаменника, тобто вирішимо рівняння. Коріння Все коріння прості, тому можна скористатися формулою (9.17). У знаменника виразу для два кореня, отже
,
;
; ,
Знаменник функції має ще третій нульовий корінь, тоді
,
; ;
; .
В результаті отримуємо
Напруга на котушці і джерелі
,
; .
Графіки залежностей струмів в гілках показані на рис. 9.12, а, а напружень на котушці і конденсаторі - на рис. 9.12, б.

1. Зображення вхідної напруги (див. Таблицю 9.1). Початкові умови - нульові.
2. Операційна схема показана на рис. 9.14. Операторний зображення струму
3. Перехід до оригіналу виконаємо по теоремі розкладання. Коріння знаменника.
Якщо знаменник має простих коренів і корінь кратності (однакових коренів), то теорема розкладання записується у вигляді (9.19). Зокрема при двох однакових коренях вираз (9.19) має вигляд
Для простого кореня відповідно до теореми розкладання
.
Об'єднуючи складові, отримаємо шуканий струм
Перехід можна виконати за таблицею 9.1.
Потрібно визначити закон зміни напруги на конденсаторі для ланцюга, зображеної на рис. 9.15. До ланцюга докладено синусоїдальна напруга параметри елементів ланцюга: мкФ; Ом. При розрахунку використовувати комплексне зображення синусоїдальної напруги.
1. Розрахунок усталеного режиму до комутації здійснюється символічним методом:
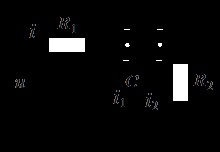
Операторний зображення вільної складової струму
.
Коріння многочлена знаменника:
Перехід від зображень до оригіналів виконаємо по теоремі розкладання. Вільна складова струму:
Вираз для струму в ланцюзі запишемо як суму вільної і змушений складових струму:
1. Запишіть формули прямого і зворотного перетворення Лапласа.
2. Сформулюйте властивості перетворення Лапласа.
3. Як визначити оригінал по годині?
4. Як визначити зображення за відомим оригіналу?
5. Сформулюйте теорему про розкладання і опишіть порядок її застосування.
6. Запишіть рівняння Кірхгофа і рівняння ідеальних елементів в операторної формі.
7. Як скласти операторної схему для розрахунку перехідного процесу?
8. Як скласти операторної схему для розрахунку вільної складової перехідного процесу?
9. Який порядок розрахунку операторної схеми заміщення?
9. Які методики розрахунку перехідного процесу операторних методом?
11. Сформулюйте переваги і недоліки операційного методу і кожної з методик окремо.