Прилади для спектральних спостережень
Якщо розкласти сонячне світло в спектр, то відкривається можливість отримати з нього значно більшу інформацію.
Розглянемо, за допомогою яких приладів можна побудувати спектр Сонця.
Зі шкільного курсу фізики відомо, що в пучку білого світла промені різних довжин хвиль йдуть в одному напрямку. Якщо на шляху такого пучка поставити диспергирующий елемент, то промені різних довжин хвиль будуть по різному відхилятися від початкового напрямку. На цьому принципі засновані всі спектральні прилади. Як диспергирующих елементів найчастіше використовують призми і дифракційні решітки. На рис. 10 показано, як проходять промені світла через призму. Зліва на призму падає пучок білого світла. Верхнє на нашому кресленні ребро призми називається заломлюючим ребром. Промінь світла, падаючи на призму, потрапляє в середовище з іншим коефіцієнтом заломлення і змінює свій напрямок. Так як коефіцієнт заломлення п залежить від довжини хвилі, то кут відхилення променя в призмі буде різним для різних довжин хвиль, З призми вийде світло у вигляді нескінченної сукупності пучків світла різних довжин хвиль, т. Е. Різного кольору, близько віддалених один від одного, і замість увійшов в призму білого пучка ми отримаємо перпендикулярну переломлюються ребру призми забарвлену смужку, в якій кольори змінюються від червоного до фіолетового.
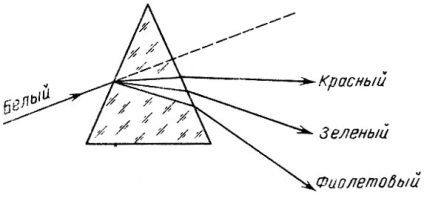
Мал. 10. Проходження світла через призму
Але одна призма не дозволяє отримати якісний спектр Сонця. Для цього потрібен спектрограф, в якому крім диспергуючого елемента є ще щілину, коліматор і камера. Оптична схема спектрографа з призмою показана на рис. 11. У лівій частині малюнка зображена вхідна щілина спектрографа, перпендикулярна до площини креслення. На телескопі вона повинна бути розташована в фокальній площині, і на ній будується зображення Сонця. Щілина є джерелом світла для спектрографа. Від неї йде конус білого світла, кут р якого визначається відносним отвором телескопа D / F де D - діаметр об'єктива або головного дзеркала телескопа, a F еквівалентна фокусна відстань телескопа. Лінза L, у фокусі якої перебуває щілину, називається коллиматором. Після коллиматора ми маємо паралельний пучок білого світла, що падає на призму. Як ми говорили вище, з призми вийде система паралельних монохроматичних (т. Е. Однієї довжини хвилі) пучків, в різному ступені відхилилися від первісного напрямку білого пучка. Кожен з цих пучків падає на лінзу L '- камеру, під своїм кутом і вони будуть зібрані цією камерної лінзою в її фокальній площині у вигляді смужки спектра, перпендикулярної переломлюються ребру. Строго кажучи, в фокальній площині камери ми отримали безперервний ряд монохроматичних зображень вхідної щілини спектрографа. Червона частина спектра розташована ближче до напрямку падаючого пучка, а фіолетова - далі від нього. Довжина отриманої смужки спектра залежить від заломлюючого кута призми, коефіцієнта заломлення того матеріалу, з якого зроблена призма, і фокусної відстані камерної лінзи L '. На рис. 11 воно позначене f '.
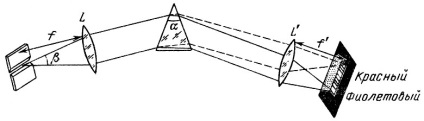
Мал. 11. Схема призменного спектрографа
Дуже важливою характеристикою, пов'язаної з довжиною спектра, є дисперсія спектрографа. Розрізняють кутову і лінійну дисперсію. Кутова дисперсія спектрографа - це похідна кута відхилення променя в призмі по довжині хвилі Зазвичай за d # 955; приймають 1 # 197; = 10 -8 см (ангстрем). Тоді кутова дисперсія - це зміна кута відхилення променя при зміні довжини хвилі на 1 # 197; (d # 949; в радіанах). Лінійна дисперсія визначається в фокальній площині камери як відстань междуо лініями спектра, довжини хвиль яких відрізняються на 1 # 197 ;,
Формула для визначення лінійної дисперсії призменного спектрографа виглядає так:
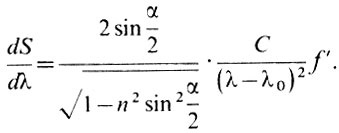
тут # 945; - заломлює кут призми, n - коефіцієнт заломлення скла, з якого зроблена призма, # 955; - довжина хвилі, З і # 955; 0 - постійні величини. Вони залежать від сорту скла.
З цієї формули видно, що дисперсія призми обернено пропорційна довжині хвилі. Звідси випливає, що червона частина спектра буде стиснута, а синя розтягнута.
Диспергирующим елементом може бути і дифракційна решітка. Як правило, вона являє собою товсту плоскопараллельную пластину з напиленням у вакуумі шаром алюмінію на одній поверхні. На цій поверхні спеціальним алмазним різцем нанесені паралельні борозенки - штрихи решітки. Кількість штрихів на різних решітках буває різний - від 50 до 1200 на міліметр. Розкладання в спектр падаючого на такі грати світла відбувається під дією двох фізичних законів: дифракції світла на щілини (штриху в даному випадку) і інтерференції променів, відбитих від кожного штриха. Ми не будемо тут зупинятися на теорії дифракційних грат, описаної в багатьох підручниках фізики. Покажемо на рис. 12, в якому напрямку йдуть відображені пучки різних кольорів при падінні на решітку білого світла. Якщо на решітку під якимось кутом падає пучок білого світла, то в напрямку відбитого за звичайним законом геометричної оптики пучка піде також білий світ, званий нульовим порядком.
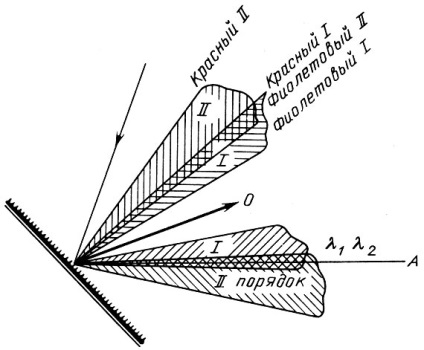
Мал. 12. Відображення світла від дифракційної решітки
Це світло відбивається дзеркальними проміжками між штрихами решітки. Світло, відбитий штрихами, дасть спектри справа і зліва від нульового порядку. На рис. 12 показано по 2 таких спектра або порядку з кожного боку. Насправді їх може бути набагато більше. На відміну від спектра, одержуваного з призмою, найменше відхиляються від напрямку білого пучка фіолетова частина спектра, а більше - червона. Особливістю спектра є і те, що кут між променями двох фіксованих довжин хвиль зростає з номером порядку. На рис. 12 видно, що кут між червоним і фіолетовим світлом в II порядку приблизно в 2 рази більше, ніж в I порядку. Ще одна суттєва характеристика спектра - накладення порядків. В одному і тому ж напрямку йдуть промені, що належать різним порядкам і мають різні довжини хвиль. Закономірність цього накладення виражається наступною простою формулою:
k # 955; k = const (константа, т. е. постійна величина).
Тут k - номер порядку, # 955; к - довжина хвилі випромінювання в k-м порядку. Пояснимо цю формулу на прикладі рис. 12. Нехай в напрямку А в I порядку решітки (k = 1) йде червоне світло довжиною хвилі # 955; 1 = 6500 # 197 ;. Тоді за формулою знаходимо значення константи const = 1 * 6500 = 6500. Підставами в вихідну формулу k = 2, знайдемо, чому дорівнює # 955; 2.
т. е. в напрямку А йде світло з II порядку з довжиною хвилі 3250 # 197 ;. Це ультрафіолетове світло, до якого наше око нечутливий, так що виявити його ми зможемо тільки за допомогою спеціальних приймачів світла.
Якщо ми хочемо спостерігати в другому і більш високих порядках решітки, то там буде накладатися випромінювання різних довжин хвиль з оптичного діапазону, т. Е. Видиме людським оком. Так, якщо в II порядку # 955; 2 = 6500 # 197 ;, к = 2, то в цьому ж напрямку з III порядку йде випромінювання що вже видно оком. Щоб розділити випромінювання різних порядків, зазвичай використовують скляні кольорові фільтри. У нашому випадку, якщо ми хочемо спостерігати червону область спектра в II порядку, треба перед щілиною, а краще після неї, помістити червоний або помаранчевий фільтр. Він не пропустить синє світло з II порядку (# 955; = 4333 # 197;). Якщо ж треба спостерігати синю область
в III порядку, слід синім фільтром "відрізати" червону частину спектру. Про характеристики скляних фільтрів буде сказано нижче.
Спектрограф з дифракційною решіткою за своєю схемою мало відрізняється від призменного спектрографа. Повинні бути присутніми ті ж основні елементи щілину, коліматор, камера. Але так як сучасні решітки в основному відбивні, то розташування цих елементів може бути іншим. На рис. 13 приведена одна з можливих оптичних схем спектрографа з гратами. Тут коллиматор і камера - увігнуті сферичні дзеркала. Фокусна відстань коліматора f а камери f '. Інша схема (рис. 14) використовує в якості коллиматора і камери один об'єктив.
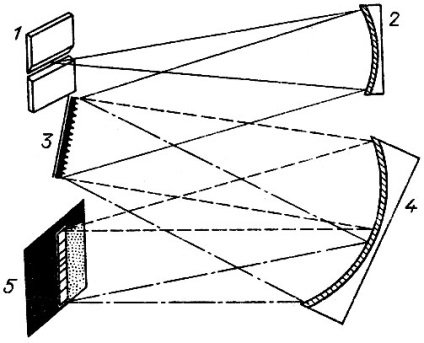
Мал. 13. Схема дифракційного спектрографа з дзеркальними коллиматором і камерою: 1 - щілина; 2 - коліматор; 3 - дифракційна решітка; 4 - камера; 5 - фокальна площина, в якій будується спектр
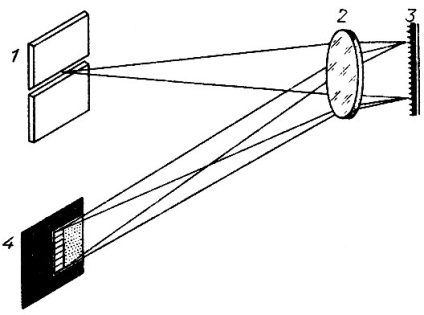
Мал. 14. Схема автоколімаційного спектрографа: 1 - щілина; 2 - об'єктив, службовець коллиматором і камерою: 3 - дифракційна решітка; 4 - фокальна площина, в якій будується спектр
Важливою характеристикою дифракційного спектрографа є його дисперсія. Для невеликих кутів падіння світла на решітку вона виражається формулою
Тут k - номер порядку спектра, з - число штрихів на 1 мм решітки, f - фокусна відстань камери в тих же одиницях, що і dl лінійне відстань в фокальній площині камери променів, що відрізняються по довжині хвилі на d # 955; (В ангстремах). Зазвичай беруть d # 955; = l # 197 ;.
Як приклад розрахуємо за цією формулою дисперсію в 1 порядку спектрографа з гратами, що має 600 штрихів на мм. Фокусна відстань камери спектрографа 7 м = 7000 мм. отримаємо
Часто користуються зворотного дисперсією, В нашому випадку
Якщо порівняти вираз для призменного і дифракційного спектрографів, то основна різниця між ними в тому, що в разі призменного спектрографа дисперсія залежить від довжини хвилі # 955 ;, а в дифракційному не залежить. У ньому дисперсія зростає при переході до більш високих порядків (пропорційно номеру порядку к).
Зупинимося на деяких особливостях спектрографа, незалежних від вибору диспергуючого елемента. Вибір тієї чи іншої схеми спектрографа, розмірів його елементів залежить значною мірою від характеристик телескопа, на виході якого буде встановлений спектрограф. Як кажуть астрономи, спектрограф повинен бути узгоджений з телескопом по світлосилі. Пояснимо це на рис. 15. Зліва умовно зображений телескоп, діаметр об'єктива якого дорівнює D, а фокусна відстань F. У фокальній площині телескопа знаходиться щілина спектрографа, праворуч від якої розташований спектрограф (на малюнку показаний тільки коллиматор). Світло, що падає на щілину спектрографа, являє собою конус з кутом розчину D / F і вершиною О на щілини. Природно, що в спектрографі від щілини світло буде поширюватися в такому ж конусі. Оптимальний розмір коллиматора треба вибирати таким, щоб весь пучок, що пройшов через щілину, пройшов і через коліматор (або відбився від нього в разі сферичного дзеркала). Ця умова рівносильна рівності D / F = d / f, т. Е. Відносні отвори (і світлосили) телескопа і коллиматора повинні бути рівні.
Мал. 15. Узгодження телескопа і спектрографа по світлосилі
Подивимося тепер, яке може бути співвідношення характеристик об'єктивів (або дзеркал) коліматора і камери. Так як, по суті справи, спектр є послідовність монохроматичних зображень вхідної щілини, які будують камера і коліматор, то розмір монохроматичного зображення щілини залежить від відносини фокусних відстаней коллиматора (f) і камери (f '). Якщо ширина щілини дорівнює а, то ширина її монохроматичного зображення буде
При великому s буде сильне переналоженіе сусідніх монохроматичних зображень, т. Е. Зменшиться чистота спектру. Зменшити s можна зменшивши f 'або збільшивши f. Вище ми наводили формули дисперсії, з яких було видно, що зі зменшенням фокусної відстані камери f 'дисперсія буде зменшуватися. Тому для збільшення чистоти спектру краще вибрати об'єктив (або дзеркало) коліматора з великим f. Що стосується ширини щілини а, то її вибір не довільний. З щойно наведеної формули видно, що чим ширше щілину, тим гірше чистота спектру. Але зі зменшенням ширини щілини в спектрограф проходить менше світла. Оптимальне значення ширини щілини, зване нормальною шириною щілини, визначається формулою
де # 955; - довжина хвилі в тих же одиницях, що і ширина щілини # 916; lN. F / D - найменший з двох відносних фокусов- телескопа і коллиматора, якщо вони не рівні. На практиці користуються шириною щілини, яка визначається за цією формулою або дещо більшою (до 2 # 916; lN).