Векторним твором векторів і називається новий вектор. наділений властивостями:
1) його довжина; а значить чисельно дорівнює площі паралелограма, побудованого на цих векторах як на сторонах;
2) вектор перпендикулярний до і;
3) вектори; і утворюють так звану поворот першого «сомножителя» проти годинникової стрілки до суміщення з другим вектор співмножником бачиться нам «з кінця» вектора найкоротшим, тобто (дивись малюнок) меншим 180º.
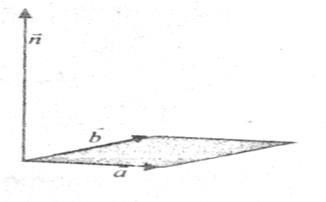
Векторний добуток позначається символами або
і має властивості:
З цих властивостей випливає
Правило обчислення векторного добутку
Для заданих в декартовом базисі векторів
їх векторний добуток може бути знайдено за формулою
З визначення і властивостей слід і
Основні програми векторного твори
Якщо S # 8710; - площа трикутника побудованого на векторах і. а # 966; - кут між ними то
Якщо h - висота піраміди (паралелепіпеда (призми)), побудованого (дивись наступний нижче малюнок) на векторах як на ребрах, то вона може бути знайдена за формулою
Змішане твір векторів.
Змішаним твором трьох векторів називається число, яке дорівнює скалярному добутку векторного твори перших двох векторів на третій.
Позначивши змішане твір символом (), за визначенням, маємо
У декартовом базисі мішаний добуток векторів
обчислюється за формулою
Геометрично модуль змішаного твори () дорівнює обсягу паралелепіпеда, побудованого на векторах як на ребрах. З цього, зокрема, випливає, що він же дорівнює подвоєному обсягом відповідне призми і «ушестеренному» обсягом піраміди з тими ж ребрами.