Напевно, кожен чув про моделях освітлення, вони оточують нас всюди: наприклад, візьмемо будь-який об'єкт, той же стакан, що стоїть на столі. На нього падає певне світло, якщо по точніше, то світло від сонця або будь-якого іншого джерела освітлення, це і називається деякої моделлю освітлення. На практиці зазвичай ніхто не намагаються запрограмувати все фізичні принципи світла, оскільки їх обчислення дуже дорого обходиться. Однак придумано безліч моделей дають реалістичний результат при малих розрахунках.
Розглянемо всі докладніше, створимо просту модель освітлення - рівномірне освітлення.
1. Рівномірне освітлення.
Рівномірне освітлення (ambient lighting) забезпечує постійне початкове освітлення для всієї сцени. Воно висвітлює всі вершини об'єктів однаково, тому що не залежить ні від яких інших чинників освітлення. Це самий простий і швидкий тип освітлення, але при цьому дає найменш реалістичний результат. Формула для обчислення цієї моделі освітлення так само дуже проста, тому що там всього одна арифметична операція - множення. Для її обчислення досить перемножити колір матеріалу на інтенсивність освітлення.
Верховий шейдер для розрахунку рівномірної моделі освітлення:
Цей найпростіший шейдер просто обчислює позицію об'єкта в світовому просторі, але в даній моделі освітлення можна його і не використовувати, оскільки від вершини нам не треба якихось інших компонентів (нормаль і т.д.) для розрахунку.
Тут теж немає нічого складного, просто повертаємо компілятору твір вектора, на яке то число в даному випадку ambient_intensity. Робить він це так:
Модель рівномірного освітлення:

Для того щоб обчислити бликовое і дифузний компоненти світла, необхідно знайти три вектори:
• Нормаль N до фрагменту.
• Видовий вектор V - вектор, який направлений на спостерігача.
• Позицію джерела світла L.
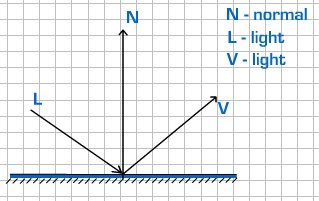
Кути між цими векторами складають інтенсивність освітлення.
2. Дифузна модель освітлення.
Дифузна модель освітлення (diffuse lighting model) - модель освітлення, яка залежить від положення джерела освітлення і від об'єктної нормалі поверхні. Оскільки випромінювання світла однаково в усіх напрямках, видовий вектор не має значення, тобто v = 0. Такий метод вимагає більшого обчислення, так як змінюється для кожної вершини об'єкта, однак непогано затінює об'єкти і надає їм обсяг. Світло падає, не заповнюючи всю поверхню однаковим кольором (як у випадку з раномерним освітленням), а створюється враження, що, світло спрямований на якусь поверхню.
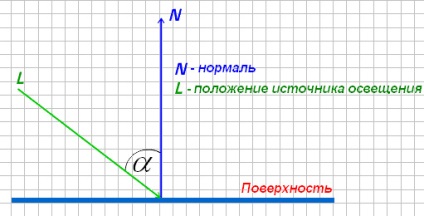
Якщо вектор позиції джерела освітлення перпендикулярний поверхні, то ніякої мат не буде спостерігатися, тому що інтенсивність світла залежить від кута # 945 ;. Для розрахунку дифузійної моделі освітлення використовується формула (за законом Ламберта):
Підіб'ємо підсумки - створимо шейдери для розрахунку освітлення.
І піксельний шейдер:
Дифузна модель освітлення:
3.Бліковая модель освітлення.
Складно, уявити таку модель освітлення не побачивши її. А насправді цю модель ми можемо побачити майже скрізь. Наприклад, чисто відполіровану (круговими рухами) пряму металеву поверхню, направивши на неї джерело світла, і подивившись під якимось кутом, що не перпендикулярний поверхні. В результаті ми побачимо відблиски на поверхні, які суттєво збільшують реалістичність зображення. Ці відблиски є відображенням джерела світла від поверхні. У цій моделі освітлення крім векторів позиції джерела освітлення і нормалі (як у випадку з дифузійної моделлю освітлення) використовуються ще два вектора: видовий вектор і вектор відображення. Бликовое модель освітлення (specular lighting model) запропонував Буї-Туонг Фонг.
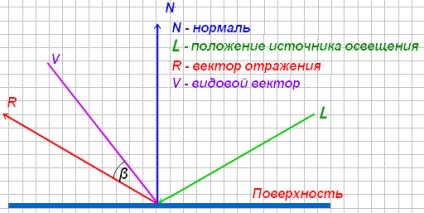
Кут між видовим вектором і вектором відображення - # 946 ;. Чим більше кут # 946 ;, тим яскравіше бликовое освітлення. Тому бликовое модель освітлення обчислюється за такою формулою:
де R = reflect (-norm (V), N)
n - коефіцієнт яскравості світіння.
Залежність яскравості світіння від кута # 946 ;:
З ростом параметра n відображення ставати все більш бликовое і все більш концентрується вздовж напрямку вектора відображення R.
Необов'язково обчислювати видовий вектор в шейдера, можна обчислити в програмі і занести в верховий шейдер. Для цього потрібно інвертувати видову матрицю і помножити на вектор D3DXVECTOR4 (0.0,0.0,0.0,1.0) - позиція при якій вектор перпендикулярний поверхні (дивиться на нас). Виглядає це так:
Бликовое модель освітлення:

Модифікація бликовое освітлення по Блінну.
Джим Блинн придумав альтернативний спосіб обчислення бликовое освітлення, який усуває дорогі обчислення над вектором відображення. Він ввів проміжний вектор, який є середнім значенням між видовим вектором і вектором позиції джерела освітлення: H = (L + V) / (| L + V |)
Загальна формула має вигляд:
Тому Фрагментний шейдер вже буде такий:
Прискорення обчислення яскравості світіння.
Шлік запропонував заміну ступеня n. Нехай скалярний добуток дорівнює D: D = (N • H) n. тоді по його способу яскравість світіння буде обчислюватися так:
Порівняльні графіки статечних законів:
Насправді фізичний зміст бликовое відбиття світла набагато складніше, ніж передбачається в моделі освітлення Фонга. У більш реалістичної моделі Is залежить від довжини хвилі l і від кута падіння світла (N • L). Така залежність називається коефіцієнтом Френеля.
Комбінування компонентів освітлення.
Тепер ми можемо скласти три моделі освітлення (постійне, дифузне і бликовое), щоб отримати сумарну кількість світла I, що отримується оком:
Піксельний шейдер тепер буде такий:
Реалістичне висвітлення на основі Кука-Торренса
У більш реальних моделях освітлення основна увага приділяється на розподіл енергії падаючого світла. Частина її поглинається матеріалом і перетворюється в тепло, інша частина розсіюється у вигляді дифузного світла, третя частина задає поверхні бликовое освітленість. Тому для різних матеріалів поділ падаючого світла відбувається по-різному, і залежить воно від:
• Функції розподілу нормалей
• Затінення і екранування
• Коефіцієнта Френеля
Функція розподіл нормалей
Ця функція описує можливе відхилення нормалі до поверхні від ідеальної нормалі N. Чим більше ця функція полога, тим більші відхилення допустимі і тим більшої величини пляма відбитого відблиску. Необхідні нормалі розташовані уздовж вектора L + V і видимі в напрямку V і знаходяться під кутом (H • N) до глядача. Кук і Торренс використовували формулу розподілу Бекмана:
де d = H • N
m - ступінь шорсткості об'єкта. 0.2f - гладка поверхня, 0.6f - шорстка. За замовчуванням ставлять 0.3f.
Графік розподілу Бекмана:
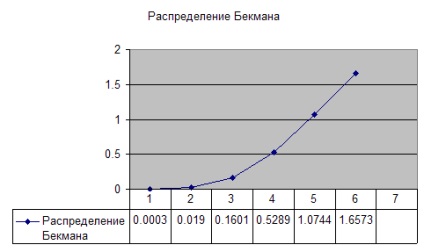
Затінення і екранування
У моделі Кука-Торренса враховуються також і такі ефекти, як затінення (shadowing) і екранування (masking), які визначають інтенсивність бликовое складової.
Неекранований світло дорівнює:
Незатененние світло дорівнює:
Тоді фінальний множник G дорівнює:
Цей коефіцієнт визначає частку відбитого світла і задається функцією:
де f - кут падіння, косинус, якого дорівнює c = (N • H)
n - показник заломлення матеріалу, g = sqrt (n 2 + c 2 -1)
Насправді, в шейдера ми будемо використовувати іншу формулу для розрахунку коефіцієнта Френеля через обмеженість інструкцій. Заміну запропонував Шлік:
F = Rs + (1-Rs) × (1 E • N) n
де Rs - бликовое відображення,
E - вектор спостерігача,
N - нормаль з карти нормалей.
Така апроксимація не враховує відповідно f і n компоненти, але має ступінь n, зі збільшенням якої можна домогтися гарних результатів. Шлік використовував n = 5.
Комбінування всіх множників
Торренс і Сперроу об'єднали ці множники і вивели формулу для підрахунку бликовое світла:
Знаменник N • V введений для регулювання інтенсивності світла.

Загальна формула для розрахунку кількості світла така:
Довелося формулу трохи спростити, так як в оригіналі кожен компонент освітлення (крім бликовое) множиться ще й на F (0, n). Зроблено це через використання апроксимації Шліка.
Піксельний шейдер цього ефекту: