Реферат на тему:
-
Вступ
- 1 Попередні відомості
- 1.1 Оцінка параметрів системи
- 1.2 Матриця експерименту
- 1.3 Рішення системи
- 1.4 Повернення до ненормованим факторам
- 2 Повний факторний експеримент
- 2.1 Матриця ПФЕ в загальному вигляді
- 2.2 Властивості матриці ПФЕ
- 2.3 Обчислення коефіцієнтів лінійної моделі
- 2.4 Перетворення природних факторів в нормовані і назад
Повний факторний експеримент (ПФЕ) - сукупність кількох вимірювань, які відповідають таким умовам:
- Кількість вимірювань становить 2 n. де n - кількість факторів;
- Кожен фактор приймає тільки два значення - верхнє і нижнє;
- В процесі вимірювання верхні і нижні значення факторів комбінуються у всіх можливих поєднаннях.
Перевагами повного факторного експерименту є
- простота рішення системи рівнянь оцінювання параметрів;
- статистична надмірність кількості вимірювань, яка зменшує вплив похибок окремих вимірювань на оцінку параметрів.
1. Попередні відомості
Апроксимація нелінійної функції двох змінних площиною
1.1. Оцінка параметрів системи
У практичній діяльності часто потрібно оцінити параметри деякої системи, тобто побудувати її математичну модель і знайти чисельні значення параметрів цієї моделі. В якості вихідних даних для побудови моделі є результати експерименту, який являє собою сукупність декількох вимірювань, виконаних за певним планом. У найпростішому випадку план є описом умов проведення вимірювань, тобто значення вхідних параметрів (факторів) під час вимірювання.
Як приклад систем, оцінка параметрів яких актуальна з практичної точки зору, можуть бути різні технологічні процеси. Для ілюстрації розглянемо процес фотолітографії.
Фотолітографія є нанесення малюнка на поверхню фотографічним методом. Вона складається з наступних етапів: підготовка поверхні, нанесення фоточутливої емульсії (фоторезиста), сушка, установка трафарету або пластини з негативним малюнком, експозиція (засвічування) ультрафіолетовими променями, травлення (прояв). Оскільки технологічні тонкощі фотолитографии в даному контексті не важливі, в якості основних факторів, що впливають на процес літографії, будемо вважати товщину фоточутливої емульсії d (в мікронах) і час експозиції t (в секундах). Вихідним параметром (відгуком) процесу вважатимемо його дозвіл R. тобто максимальну кількість помітних ліній, які можливо провести на одному міліметрі поверхні. Ця величина визначається шляхом нанесення на поверхню спеціального тестового зображення.
Отже, технологічний процес фотолітографії описується деякою функцією виду
Побудова моделі технологічного процесу дозволяє виявити поведінку відгуку системи в залежності від зміни факторів і тим самий знайти шляхи для оптимізації технології. Для даного конкретного випадку - вибрати таку товщину емульсії і час експозиції, які забезпечать найкращу якість зображення.
У загальному випадку відгук системи описується деякою функцією n змінних
Математична модель системи виходить в результаті апроксимації цієї функції будь-якої іншої функцією, наприклад лінійної
На малюнку в графічному вигляді представлений процес побудови лінійної моделі процесу фотолітографії, де x1 - товщина плівки фотоемульсії, x2 - час експонування, y - дозвіл, отримане в даних умовах. Функція y = f (x1, x2) нелінійна, проте в достатній близькості від точки A0 її можна замінити дотичній площиною y = a0 + a1x1 + a2x2. У показаної на малюнку області максимальна помилка моделі становить Δy.
Знаючи коефіцієнти моделі a0, a1, a2. можна з певною точністю передбачати значення функції (а значить і поведінку системи) в околицях точки A0. У визначенні значень коефіцієнтів a0, a1, a2 і полягає мета експерименту.
1.2. матриця експерименту
Розташування еесперіментальних точок в двомірному факторном просторі
Припустимо, вихідні параметри технологічного процесу складають: товщина плівки 55 мкм, час експозиції - 30 с, тобто
Візьмемо верхні і нижні значення обох факторів так, щоб вони розташовувалися симетрично щодо поточного значення, наприклад
Складемо таблицю, в якій значення обох факторів знаходяться у всіх можливих поєднаннях і проведемо вимірювання в цих точках (значення відгуку дані умовно):

Вважаючи, що лінійна модель процесу має вигляд
на підставі отриманих результатів можна скласти систему чотирьох рівнянь з двома змінними. Нижче показана ця система, а також її скорочений запис у вигляді матриці. Матрицю даного виду назвемо матрицею експерименту.

У матриці експерименту другий і третій стовпці представляють собою значення факторів, четвертий стовпець - значення відгуку системи, а перший стовпець містить одиниці, відповідні одиничним коефіцієнтам вільного члена моделі a0. Будемо вважати цей стовпець деяким віртуальним фактором x0. який завжди приймає одиничні значення.
1.3. рішення системи
Перехід до нормованих координатах
Щоб полегшити рішення системи, проведемо нормування факторів. Верхніх значень факторів дамо нормоване значення +1, нижнім значенням - нормоване значення -1, середнього значення - нормоване значення 0. У загальному вигляді нормування чинника виражається формулою
З урахуванням нормування факторів система рівнянь і матриця експерименту приймуть такий вигляд:
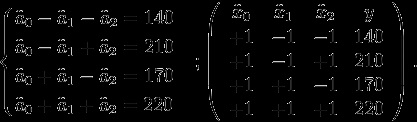
Оскільки сума членів у другому і третьому стовпці матриці дорівнюють нулю, вільний член моделі можна знайти, склавши всі чотири рівняння:
Щоб знайти який-небудь інший коефіцієнт моделі, потрібно змінити знаки в рівняннях таким чином, щоб у відповідному стовпці виявилися одні одиниці, після чого скласти всі чотири рівняння:
Таким чином, лінійна модель технологічного процесу в околицях точки (55, 30) має вигляд
У загальному випадку рішення системи буде виглядати як
1.4. Повернення до ненормованим факторам
Перехід від нормованих до ненормованим факторів здійснюється зворотним перетворенням
Щоб знайти параметри моделі для ненормованих координат, підставимо вирази для нормованих координат в рівняння моделі:
Cравнівая останній вираз з виразом для лінійної моделі в ненормованих координатах
отримаємо вирази для параметрів моделі:
Для наведеного вище прикладу
Остаточно отримуємо модель в природних координатах:
2. Повний факторний експеримент
2.1. Матриця ПФЕ в загальному вигляді
У загальному вигляді матриця повного факторного експерименту з n факторами має вигляд
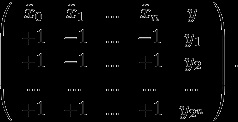
2.2. Властивості матриці ПФЕ
Матриця ПФЕ має такі властивості:
- Число рядків в матриці дорівнює 2 n;
- Нульовий стовпець матриці складається з одиниць:
- У стовпчиках 1. n знаходяться всі можливі 2 n поєднань значень -1 і +1;
- В останньому стовпці знаходяться результати вимірювань, отримані при значеннях факторів, записаних у відповідних рядках в шпальтах 1. n.
- Сума елементів нульового стовпця завжди дорівнює 2 n:
- Сума елементів будь-якого стовпця, крім нульового і останнього, дорівнює нулю:
- Два останніх вирази можна об'єднати в єдине співвідношення:
- Сума квадратів елементів будь-якого (крім останнього) стовпця завжди дорівнює 2 n:
- Сума творів відповідних елементів двох будь-яких стовпців (крім останнього) дорівнює нулю:
- Два останніх вирази можна записати як ортогональность стовпців матриці:
2.3. Обчислення коефіцієнтів лінійної моделі
Коефіцієнти лінійної моделі в нормованих координатах обчислюються за формулами:
Коефіцієнти лінійної моделі в природних (ненормованих) координатах обчислюються за формулами: