Н а цій сторінці зібрані теореми планіметрії, які репетитор з математики може використовувати в підготовці здібного учня до серйозного іспиту: олімпіаді або іспиту в МГУ (в підготовці на Мехмат МГУ, ВМК), до олімпіади в Вищій Школі Економіки, до олімпіади в Фінансової Академії і в МФТІ. Знання цих фактів відкриває перед репетитором великі можливості по складанню конкурсних завдань. Досить «обіграти» якусь згадану теорему на числах або доповнити її елементи нескладними взаємозв'язками з іншими математичними об'єктами, і вийде цілком пристойна олімпіадних завдання. Багато властивостей присутні в сильних шкільних підручниках як задач на доказ і спеціально не виносяться в заголовки і розділи параграфів. Я постарався виправити цей недолік.
Математика - неосяжний предмет, а кількість фактів, які можна виділяти як теореми - нескінченно. Репетитор з математики не може фізично знати і пам'ятати всі. Тому якісь хитрі взаємозв'язку між геометричними об'єктами кожен раз відкриваються викладачеві заново. Зібрати всі їх на одній сторінці відразу - неможливо фізично. Тому я буду заповнювати сторінку поступово, у міру використання теорем на своїх уроках.
Раджу початківцям репетиторів з математики бути обережніше у використанні додаткових довідкових матеріалів, оскільки більшість цих фактів школярі не знають.
Репетитор з математики про властивості геометричних фігур
1)
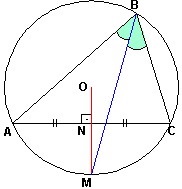
2)
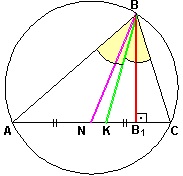
3)
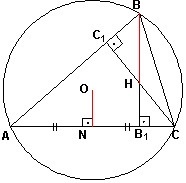
4)
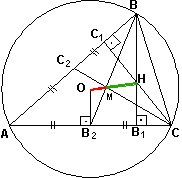
5)
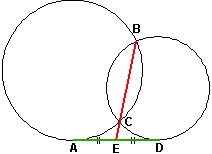
6)
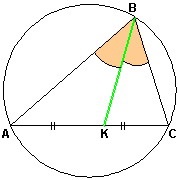
Тобто має місце рівність
7)
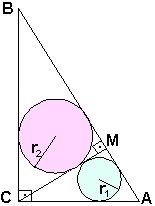
8)
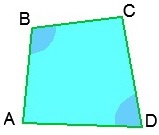
, де x - сума будь-яких двох протилежних кутів чотирикутника. Якщо даний чотирикутника є вписаною в коло, то і формула набуває вигляду:
і називається формулою Брахмагупти
9) Якщо ваш чотирикутник описаний близько окружності (тобто коло в нього вписана), то площа чотирикутника обчислюється за формулою
10)
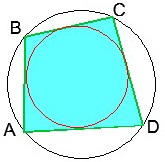
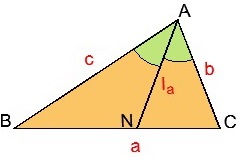
11)
Досвідченому репетитора, щоб не втратити кваліфікацію, я раджу регулярно переглядати варіанти олімпіад незалежно від складу поточних учнів. Перш за все для підтримки відповідного рівня розвитку. Заглядайте в довідники та енциклопедії. Розширюйте свій кругозір і удосконалюйтеся! Для цього зроблено дана сторінка!
При наявність додаткових знань геометричних фактів репетитор з математики надасть вагому допомогу учневі в пошуку швидких рішень. Наприклад, таку допомогу можна отримати у мене в Строгіно. У перспективі, при щільній роботі з завданнями це призведе до зниження часу на вирішення завдання С4 на ЄДІ з математики. На ЄДІ можна вирішувати завдання будь-яким правильним способом, навіть із застосуванням засобів і властивостей, що не входять до шкільної програми (в тому числі методами вищої математики).
З глибокою повагою, Колпаков А.Н.
Кваліфікований репетитор з математики. Строгіно. м.Щукінская. Підготовка до будь-яких видів іспитів, а також до олімпіад.
Дякуємо. Матеріали сайту оформлені є і барвисто, часто використовую їх при вирішенні домашніх завдань. На жаль, живу в іншому місті і немає можливості найняти репетитора. У школі дають мінімум і тому для мене багато теореми з цієї сторінки були не знайомі.
Випадково натрапив на сайт. Дуже приємний, легкий, білий. Зайшов за запитом - точка перетину висот.
Ось якби були докази, було б набагато легше.