Ланцюг з послідовно з'єднаних індуктивності, ємності і активного опору може розглядатися як коливальна система, так як в ній можливе виникнення електромагнітних коливань з власною частотою
Ці коливання є затухаючими, так як енергія, зосереджена в контурі в момент виникнення коливань виділяється у вигляді тепла на активному опорі під час коливального процесу.
Тоді, при включенні в контур джерела змінної ЕРС, його можна розглядати як елемент, який ініціює в контурі вимушені коливання з частотою. Отже, рівняння
являє собою рівняння вимушених електромагнітних коливань під дією зовнішньої періодично змінюється ЕРС.
Використовуючи фізичні величини: власну частоту і коефіцієнт загасання це рівняння можна представити і у вигляді.
Як відомо, для вимушених коливань характерне явище резонансу, яке полягає в зростанні амплітуди вимушених коливань при наближенні частоти зовнішнього впливу до резонансної частоти, що залежить від параметрів коливальної системи.
У розглянутій ланцюга - коливальному контурі вимушені коливання здійснюють сила струму, заряд і напруга на конденсаторі, а також напруга на котушці індуктивності.
Резонансними кривими називаються залежності амплітудних значень, що здійснюють вимушені коливання фізичних величин, від частоти зовнішнього впливу, т. Е. В нашому випадку, від частоти джерела ЕРС.
Закон Ома для даної ланцюга - коливального контуру дозволяє проаналізувати залежність амплітуди сили струму від частоти джерела ЕРС:.
Якщо амплітудне значення ЕРС, а також величини активного опору, ємності й індуктивності постійні, то амплітудне значення сили струму залежить тільки від частоти.
Максимальна амплітуда сили струму: при. В цьому випадку частота джерела ЕРС збігається з власною частотою коливального контуру:,
т. е. для вимушених коливань сили струму спостерігається резонанс.
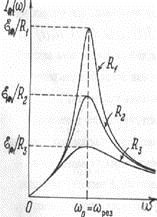
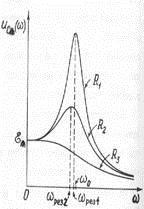
На ріс.155 показані резонансні криві для амплітуди сили струму в залежності від частоти джерела при різному активному опорі коливального контуру. Резонанс виражений тим виразніше, чим менше активний опір, т. Е. Чим менше коефіцієнт загасання.
Коливання заряду і напруги на конденсаторі збігаються по фазі. Знайдемо залежність амплітуди коливань заряду від частоти. Як показано в § 51. Якщо використовувати вирази для власної частоти і коефіцієнта загасання, то цей вислів перетвориться до виду:
. Максимальне значення амплітуди заряду досягається при мінімальному значенні подкоренного вираження. Візьмемо похідну від подкоренного вираження по частоті і прирівняємо її нулю: або. Підставивши це значення у вираз для амплітудного значення заряду, отримаємо:.
Так як . то максимальна амплітуда напруги на конденсаторі досягається при тому ж значенні частоти джерела ЕРС:.
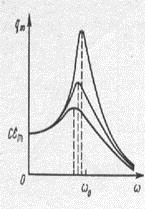
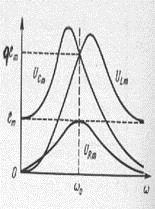
На ріс.156 і ріс.157 показані резонансні криві для амплітудних значень заряду і напруги на конденсаторі при різних активних опорах контуру.
Резонансна частота для заряду і напруги завжди менше, ніж резонансна частота для струму, а резонанс виражений тим більше, чим менше активний опір контуру.
РІС.155 РІС.156 РІС.157 РІС.158
Максимальне значення напруги на котушці індуктивності (см.§ 51) перетворимо також, використовуючи поняття власної частоти і коефіцієнта загасання:
. Резонансну частоту можна знайти, взявши похідну по частоті від цього виразу і прирівнявши її до нуля. Резонансна частота для напруги на котушці індуктивності дорівнює:.
Якщо перетворити і порівняти вирази для резонансних частот на конденсаторі і на котушці індуктивності з резонансною частотою струму:. . . то можна зробити висновок, що, загалом випадку, резонансна частота для напруги на конденсаторі завжди менше, а для напруги на котушці індуктивності завжди більше, ніж резонансна частота для сили струму (і напруги на активному опорі). Резонансні криві для напруг на активному опорі, котушці індуктивності і ємності показані на ріс.158.
Для представляють практичний інтерес контурів з малим загасанням,. членом Можна знехтувати. В цьому випадку резонанс для всіх змінних електричних величин: сили струму, заряду і напруги на конденсаторі, напруги на котушці індуктивності настає практично одночасно при частоті джерела, рівній частоті вільних коливань в контурі:
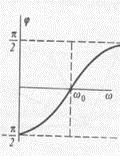
. При резонансі зсув фаз між струмом і напругою дорівнює нулю (ріс.159).
Для контурів з великим загасанням, якщо активний опір таке велике, що. подкоренное вираз стає уявним і резонансна крива не має максимуму, т. е. резонанс відсутній. В цьому випадку, залежність, наприклад, напруги на конденсаторі від частоти джерела представлена на ріс.157 для опору R3.
Розглянуте явище резонансу при послідовному з'єднанні джерела з елементами контуру називається резонансом напруг. При цьому - називається хвильовим або характеристичним опором, а максимальні напруги на котушці індуктивності і конденсаторі рівні й протилежні по фазі.
Для контурів з малим загасанням характерний «гострий» резонанс і висока добротність. яка (см.§ 50) характеризує відносну спад енергії контуру за період при вільних коливаннях.
Фізичний сенс добротності для контурів з малим загасанням при резонансі.
1) Добротність показує у скільки разів максимальне значення амплітуди напруги на конденсаторі (і на індуктивності) перевищує амплітуду зовнішньої ЕРС (ріс.158). .
Отже, необхідно враховувати, що при резонансі, навіть при невеликій зовнішньої ЕРС, напруги на індуктивності і ємності можуть досягати великої величини, небезпечної для життя людини:
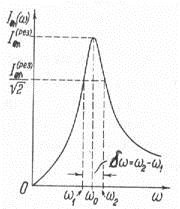
2) Можна показати, що добротність характеризує відносну ширину резонансної кривої:. Шириною резонансної кривої, або смугою пропускання називається інтервал частот. обмежений частотами і. на яких амплітуда в Менше амплітуди при резонансі (ріс.160).
Отже, добротність - величина зворотна відносної ширині пропускання або відносної ширині резонансної кривої.
Резонанс використовується для виділення зі складного «сигналу» (зареєстрованого напруги) необхідною складовою. Це має практичне значення в радіотехніці при прийомі і настоянці на певну частоту радіосигналу. Чим вище добротність контуру, тим вже резонансна крива і тим легше «відбудовуватися» від передач, що ведуться на сусідніх частотах.
На практиці добротність контуру підбирається і з обліків необхідної якості прийому сигналу, так як з зменшення ширини резонансної кривої зменшується інформація (діапазон частот) «пропускається» контуром.