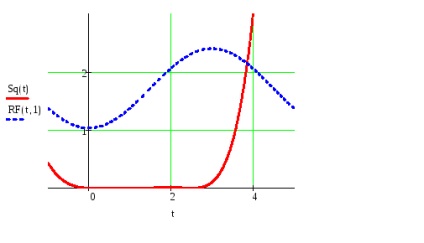
Дана Т - періодична функція f (t)
Обгрунтувати можливість розкладання f (t) в ряд Фур'є, встановити вид збіжності ряду Фур'є до f (t).
Теорема Діріхле: Якщо Т - періодична функція f (t) задовольняє умовам Діріхле на будь-якому замкнутому інтервалі довжиною Т:
Неперервна або має кінцеве число точок розриву першого роду
Монотонна або має кінцеве число максимумів і мінімумів
Ряд Фур'є сходитися на всій осі t і сума ряду Фур'є одно f (t) у всіх точках безперервності цієї функції в точці t0 розриву першого роду функції f (t) сума ряду Фур'є дорівнює дана функція f (t) задовольняє умовам збіжності в середньому.
Ознака Ляпунова: Якщо Т - періодична функція f (t) задовольняє умовам для кусково-неперервна і інтегрована з квадратом, то ряд Фур'є сходитися середньоквадратичне до f (t).
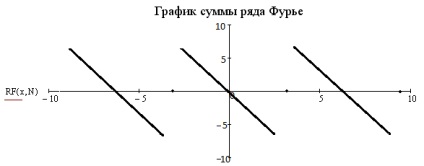
Побудувати графік суми ряду Фур'є.
Уявити задану функцію тригонометричним рядом Фур'є, попередньо:
б) обчислити коефіцієнти ряду Фур'є.
Коефіцієнти ряду Фур'є
Тригонометричне розкладання ф-ії в ряд Фур'є
Побудувати амплітудний і фазовий спектри функції.
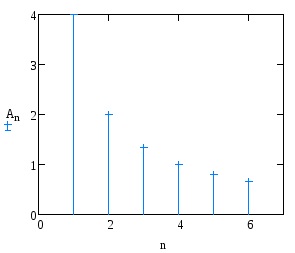
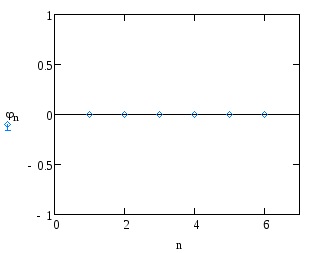
Визначити число гармонік розкладання функції в ряд Фур'є, що містять в сумі не менше 90% енергії.
Щоб визначити число гармонік, що містять в сумі не менше 90% енергії, спочатку розрахуємо енергію, що вноситься кожною гармонікою в окремо за такою формулою:
Внесок гармонік в енергію
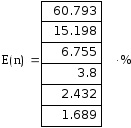
Обчислити середньоквадратичнепомилку між вихідною функцією f (t) і часткової сумою Фур'є для t, що належать проміжку завдання.
Формула для обчислення середньоквадратичної помилки:
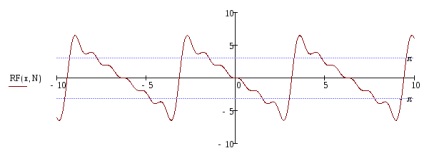
Побудувати графіки заданої функції і часткової суми ряду Фур'є для значень t, що належать проміжку завдання f (t), взявши число гармонік, визначених у пункті №5.
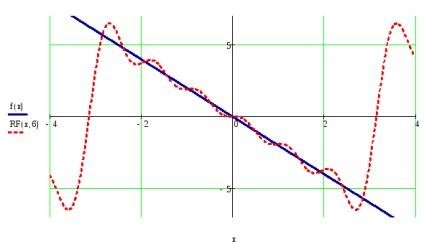
Побудувати графік квадрата відхилень функції і часткової суми ряду для t з проміжку завдання f (t).
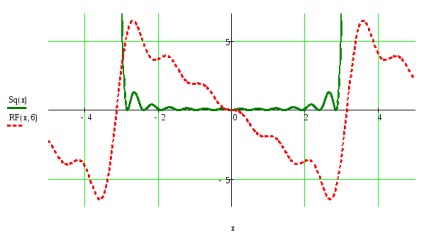
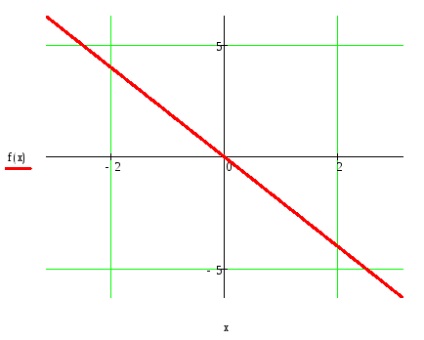
Для функції, заданої на кінцевому інтервалі, побудувати періодичне продовження заданим чином.
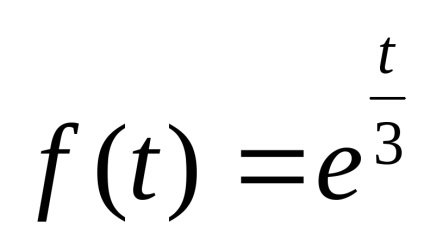
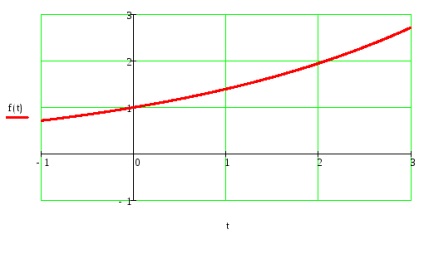
Обгрунтувати можливість розкладання f (t) в ряд Фур'є, встановити вид збіжності ряду Фур'є до f (t).
Ця функція f (t) задовольняє умовам теореми Діріхле:
Теорема Діріхле: Якщо Т - періодична функція f (t) задовольняє умовам Діріхле на будь-якому замкнутому інтервалі довжиною Т:
Неперервна або має кінцеве число точок розриву першого роду
Монотонна або має кінцеве число максимумів і мінімумів
Ряд Фур'є сходитися на всій осі t і сума ряду Фур'є одно f (t) у всіх точках безперервності цієї функції в точці t0 розриву першого роду функції f (t) сума ряду Фур'є дорівнює дана функція f (t) задовольняє умовам збіжності в середньому.
Теорема Вейєрштрасса: якщо Т - періодична функція f (x) на будь-якому замкнутому інтервалі. Наприклад [-T / 2, T / 2] задовольняє умовам: безперервності і f (-T / 2) = f (T / 2), то тригонометричний ряд Фур'є сходитися до f (x) рівномірно.
Побудувати графік суми ряду Фур'є.
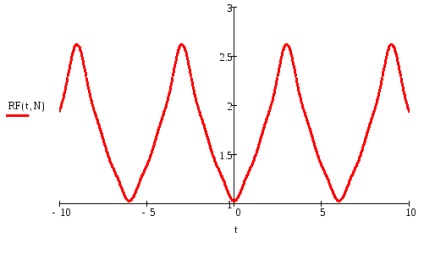
Уявити задану функцію тригонометричним рядом Фур'є, попередньо:
б) обчислити коефіцієнти ряду Фур'є
Коефіцієнти ряду Фур'є
Тригонометричне розкладання ф-ії в ряд Фур'є
Побудувати амплітудний і фазовий спектри функції.
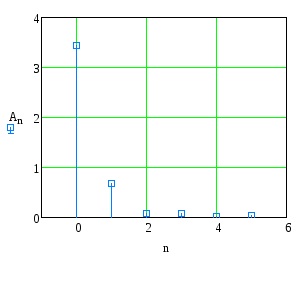
Визначити число гармонік розкладання функції в ряд Фур'є, що містять в сумі не менше 90% енергії.
Внесок гармонік в енергію
Обчислити середньоквадратичнепомилку між вихідною функцією f (t) і часткової сумою Фур'є для t, що належать проміжку завдання.
Побудувати графіки заданої функції і часткової суми ряду Фур'є для значень t, що належать проміжку завдання f (t), взявши число гармонік, визначених у пункті №5.
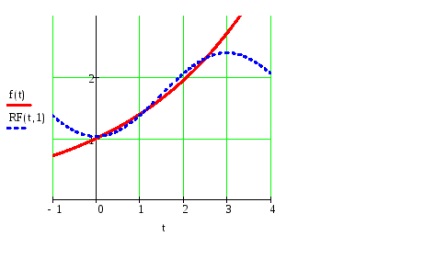
Побудувати графік квадрата відхилень функції і часткової суми ряду для t з проміжку завдання f (t).