
Завдання В1. Парашутист стрибнув з висоти h = 1200 м над поверхнею Землі без початкової вертикальної швидкості. Протягом проміжку часу Δt1 = 6,0 c парашутист вільно падав, потім парашут розкрився і протягом нехтує малого проміжку часу швидкість парашутиста зменшилася. Подальше зниження парашутиста до моменту приземлення відбувалося з постійною за модулем вертикальної швидкістю v. Якщо рух з розкритим парашутом відбувалося протягом проміжку часу Δt 2 = 92 c. то модуль вертикальної швидкості v при цьому русі дорівнював ....
За час вільного падіння без початкової вертикальної швидкості парашутист пролетів відстань:
Якщо v - швидкість парашутиста після розкриття парашута, то відстань, яке парашутист пролетів з розкритим парашутом, так само:
Так як сума цих відстаней дорівнює висоті, з якої стрибав парашутист, то
Звідси висловлюємо швидкість зниження з розкритим парашутом:
Підставляємо числові значення:
Завдання В2. На горизонтальному підлозі ліфта, що рухається зі спрямованим вниз прискоренням, стоїть валіза масою m = 30 кг, площа підстави якого S = 0,080 м 2. Якщо тиск, який чиниться валізою на підлогу, p = 2,4 кПа, то модуль прискорення a ліфта дорівнює ... .
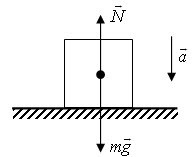
Розглянемо сили, що діють на валізу. Це сила тяжіння і сила реакції опори. Під дією цих сил валізу рухається з прискоренням, рівним прискоренню ліфта і спрямованим вниз.
Запишемо для валізи рівняння другого закону Ньютона:
Спроектуємо це рівняння на вісь Oy.
Сила реакції опори по третьому закону Ньютона дорівнює вазі валізи, який можна знайти, знаючи тиск валізи на підлогу ліфта і площа підстави валізи:
Підставляємо числові значення:
Завдання В3. На горизонтальній прямолінійній ділянці сухий асфальтованої дороги водій застосував екстрене гальмування. Гальмівний шлях автомобіля до повної зупинки склав s = 31 м. Якщо коефіцієнт тертя ковзання між колесами і асфальтом μ = 0,65, то модуль швидкості v0 руху автомобіля на початку гальмівного шляху дорівнює ....
При екстреному гальмуванні колеса автомобіля блокуються, і він починає ковзати по дорозі. На автомобіль при цьому діють сили тяжіння, реакції опори і сила тертя ковзання. Прискорення автомобіля направлено вздовж дороги.
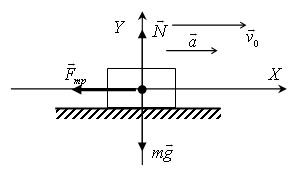
Запишемо для автомобіля рівняння другого закону Ньютона:
Спроектуємо це рівняння на осі системи координат:
З другого рівняння знаходимо реакцію опори:.
Знаючи реакцію опори, знаходимо силу тертя за законом сухого тертя:
Тоді проекція прискорення руху автомобіля:
Знак «-» говорить про те, що проекція прискорення спрямована протилежно напрямку осі Ox.
Хочу зауважити, що наведена схема є загальною для вирішення завдань на динаміку. Звичайно, можна було отримати прискорення набагато швидше, однак, в більш складних завданнях саме скрупульозний облік сил, запис другого закону Ньютона у векторній формі і в проекціях на осі координат дозволяють уникнути помилок. Крім того, я завжди рекомендую невідомі векторні величини (в даному випадку прискорення) направляти вздовж позитивних напрямків осей координат - тоді знак результату вкаже Вам справжнє напрям вектора.
Отже, ми знайшли проекцію прискорення. На цьому роль динаміки закінчилася. Знаючи прискорення руху, можемо пов'язати переміщення автомобіля і його швидкості на початку і в кінці шляху:
Зверніть увагу, що записана формула дає саме зміна координати (переміщення), а не шлях. Однак, якщо тіло рухається по прямій без розворотів, то шлях дорівнює переміщенню.
Підставляємо в записану формулу відомі величини, враховуючи, що V2x = 0 (в кінці шляху автомобіль зупинився):
Завдання В4. На гладкій горизонтальній поверхні лежить брусок масою m1 = 52 г, прикріплений до стіни невагомою пружиною жорсткістю (див. Рис.). Пластиліновий кульку масою m1 = 78 м летить горизонтально уздовж осі пружини зі швидкістю, модуль якої, потрапляє в брусок і прилипає до нього. Максимальне стиснення пружини | Δl | одно ... мм.
Завдання будемо вирішувати в два етапи: спочатку, за допомогою закону збереження імпульсу, визначимо швидкість бруска з прилиплим до нього кулькою після зіткнення, а потім за допомогою закону збереження енергії знайдемо деформацію пружини.
Часто учні пропонують вирішувати такого роду задачі, відразу використовуючи закон збереження енергії: прирівняти кінетичну енергію налітаючого кулі і потенційну енергію стиснутої пружини. Такий підхід є хибним! Справа в тому, що при непружного ударі механічна енергія не зберігається - частина її переходить в тепло, а ось імпульс зберігається навіть при непружного ударі, тому такі завдання потрібно вирішувати в два етапи.
Отже, проекція імпульсу налітаючого кулі на горизонтальну вісь p1x = m2v. Нехай v1 - швидкість бруска з кулькою після злипання, тоді проекція імпульсу системи на горизонтальну вісь дорівнює: p2x = (m1 + m2) v 1.
На підставі закону збереження імпульсу:
Тепер скористаємося законом збереження енергії для знаходження стиснення пружини.
У момент початку руху бруска кінетична енергія системи дорівнює
Потенційна енергія пружини в цей момент дорівнює нулю, так як пружина розтягнута.
Тоді повна механічна енергія системи в початковий момент часу дорівнює:
У момент максимального стиснення пружини брусок з кулькою зупиняються, тому кінетична енергія дорівнює нулю, а потенційна енергія дорівнює енергії стислої пружини. Повна енергія при цьому дорівнює
На підставі закону збереження повної механічної енергії E2 = E1. отримуємо
Підставляємо числові значення:
Завдання В5. У посудині об'ємом V = 25.0 л знаходиться газова суміш, що складається з гелію, кількість речовини якого v1 = 2.00 моль, і кисню, кількість речовини якого v2 = 0.800 моль. Якщо абсолютна температура газової суміші Т = 290 К, то тиск p цієї суміші одно ... кПа.
Для знаходження тиску в суміші газів використовують закон Дальтона. Згідно з цим законом, тиск в суміші газів дорівнює сумі парціальних тисків кожного з компонент суміші. Парціальний тиск - це такий тиск, який був би в газі, якби цей газ був в посудині один.
У нас два газу. Парціальний тиск кожного з них знайдемо за допомогою закону Менделєєва-Клапейрона:
Знаходимо тиск у суміші:
Завдання В6. Вода об'ємом V = 250 см 3 остигає від температури t1 = 98 ° C до температури t2 = 60 ° C. Якщо кількість теплоти, що виділяється при охолодженні води, повністю перетворити в роботу по підняттю будівельних матеріалів масою m = 1 т, то вони можуть бути підняті на максимальну висоту h. рівну ... дм
Кількість теплоти, що виділяється при охолодженні води, визначається за формулою:
Масу води можемо визначити, знаючи обсяг і щільність:
Якщо вся енергія, що виділилася при охолодженні води, піде на підняття вантажу, то, взагалі кажучи, висота підняття буде залежати від того, як піднімати цей вантаж: з прискоренням або без, адже якщо вантаж піднімається з прискоренням, то частина енергії йде на розгін вантажу , а частина на подолання сил тяжіння. В умови просять знайти максимальну висоту підняття. Максимально можливу висота буде в тому випадку, якщо підняття здійснюється рівномірно, тобто з прискоренням, рівним нулю.
Робота, необхідна для підняття тіла маси m на висоту h без прискорення дорівнює різниці потенційних енергій тіла:
Так як все виділилося кількість теплоти йде на підняття вантажу, то Q = A. Тоді
Підставляємо числові значення:
Завдання В7. Температура нагрівача ідеального теплового двигуна на Δt = 100 ° C більше температури холодильника. Якщо температура холодильника t = 100 ° C. то термічний коефіцієнт корисної дії η двигуна дорівнює ...%.
ККД ідеального теплового двигуна визначається за формулою Карно:
Завдання В8. На катод вакуумного фотоелемента, виготовленого з нікелю (Aвих = 4,5 еВ). падає монохроматичне випромінювання. Якщо фототок припиняється при затримувати напрузі Uз = 7.5 B. то енергія Е падаючих фотонів дорівнює ... еВ.
Запишемо рівняння Ейнштейна для фотоефекту:
Тут Т - це кінетична енергія вилетів електрона.
Затримує напруга - це така напруга, при якому фототок припиняється. Коли електрон проходить затримує напруга, електричне поле здійснює над ним роботу:
, де e - заряд електрона.
Ця робота йде на зміну кінетичної енергії електрона:
Тут ми врахували, що кінцева кінетична енергія електрона дорівнює нулю (він зупиняється).
Зверніть увагу, що в отриманому виразі робота виходу і енергія електрона записані в Джоулях. Для перекладу енергетичних величин в електрон-вольти їх необхідно розділити на заряд електрона e. Тоді енергія електрона в електрон-вольтах дорівнює:
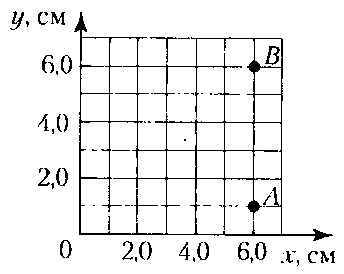
Потенціал електростатичного поля, створюваного точковим зарядом, в точці, що знаходиться на відстані r від заряду визначається за формулою:
У нашому випадку відстань між точками А і В дорівнює:
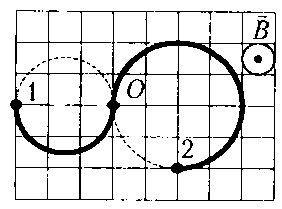
При русі зарядженої частинки в магнітному полі на частку діє сила Лоренца, яка завжди перпендикулярна швидкості частинки. Сила, перпендикулярна швидкості не змінює швидкість за величиною, а лише змінює напрямок вектора швидкості. В результаті, частка буде рухатися по колу.
Для опису зазначеного руху запишемо для частинки рівняння другого закону Ньютон, враховуючи, що рух по колу з постійною швидкістю - це рух з доцентрові прискоренням:
, де R - радіус кола.
Запишемо рівняння другого закону Ньютона для частки:
Врахуємо, що при русі по колу з постійною швидкістю, швидкість частинки можна виразити через кутову швидкість:
Запишемо отримане співвідношення для двох частинок, описаних в умові завдання:
Тут ми врахували, що заряди у частинок однакові.
Розділимо перший вираз на друге, отримаємо:
Таким чином, кутова швидкість руху частинки по колу в магнітному полі обернено пропорційна масі частинки. Це і дозволить нам знайти відношення мас частини.
З малюнка видно, що за один і той же час, іон 1 пройшов половину окружності, а іон 2 три чверті. Це означає, що кутова швидкість іона 2 більше, ніж кутова швидкість іона 1, причому
Завдання В11. В ідеальному LC -контур, що складається з котушки індуктивністю L = 27 мГн і конденсатора ємністю С = 0,50 мкФ, відбуваються вільні електричні коливання. Якщо повна енергія контуру W = 54 мкДж, то в момент часу, коли заряд конденсатора q = 4,5 мкКл, сила струму I в котушці дорівнює ... мА.
Повна енергія контура W завжди дорівнює сумі енергій електростатичного поля конденсатора і магнітного поля котушки.
Звідси знаходимо струм:
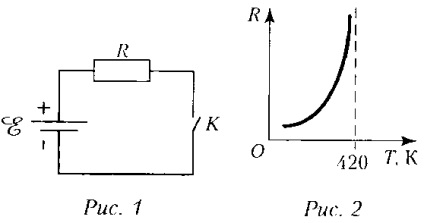
Для вирішення завдання скористаємося законом збереження енергії.
Нехай по ланцюгу пройшов заряд, рівний q. Джерело напруги при цьому зробив роботу, рівну
, так як ЕРС - це робота по переміщенню одиничного заряду по ланцюгу.
Робота, досконала джерелом йде тільки на нагрів резистора, адже за умовами задачі теплообмін з навколишнім середовищем відсутній. Резистор ж може нагрітися лише до температури 420 К. Подальший нагрів неможливий, так як опір резистора стане нескінченно великою, і струм в ланцюзі припиниться.
Для нагріву резистора від температури T0 до температури T необхідно кількість теплоти, що дорівнює
Складаємо рівняння теплового балансу:
Підставляємо числові значення: