Величина qV (z) відповідає зміні потенційної енергії позитивного заряду в ОПЗ щодо значення цієї енергії в обсязі напівпровідника (при z, яка прагне до нескінченності).
Розподіл індукованого заряду в шарі деякої товщини означає, що потенціал в напівпровіднику плавно згасає від деякого значення на поверхні до нульового значення за межами ОПЗ. Величина розподіленого об'ємного заряду # 961; (z) і потенціал електростатичного поля в ньому V (z) взаємно однозначносвязани між собою рівнянням Пуассона
де # 949; 0 - діелектрична проникність вакууму;
# 949; s - діелектрична проникність напівпровідника.
На величину qV (z) ОПЗ зміщується все енергетичні рівні, які існували в напівпровіднику в даній точці z при відсутності індукованого заряду.
Якщо виразити зміна потенційної енергії в одиницях k0 T і ввести позначення Y (z) = qV (z) / (k0 T), то рівняння Пуассона набуде вигляду
Як відомо, при певних граничних умовах вирішенням цього рівняння є деяка функція Y (z), загасаюча вглиб напівпровідника. На величину цієї функції зміщуються всі безрозмірні (в одиницях k0 T) енергетичні рівні щодо своїх безрозмірних значень до виникнення ОПЗ. Ця ж величина визначає безрозмірний вигин енергетичних зон в кожній точці z.
Величина Y (z) носить назву безрозмірного поверхневого електростатичного потенціалу.
Відстань від середини забороненої зони до рівня Фермі позначається буквою # 981 ;, а його значення на поверхні - # 981; s. На відміну від безрозмірного електростатичного потенціалу # 981; s носить назву поверхневого потенціалу. Взагалі в науковій літературі з напівпровідників індекс s прийнятий для позначення величини, що відноситься до поверхні, так як s - перша буква англійського слова «surface».
Відповідно до плавним загасанням потенціалу плавно змінюється положення всіх рівнів щодо рівня Фермі, який, як відомо, є мірою середньої енергії носіїв заряду по всьому кристалу і тому залишається незмінним аж до кордону кристала (поверхні) при z = 0.
На рис.4.3 приведена енергетична діаграма ОПЗ. Значення безрозмірного електростатичного потенціалу на поверхні позначається Ys. Знак для цієї величини відповідно до прийнятого напрямком відліку енергії буде позитивним для вигинів зон вниз і негативним для вигинів вгору.
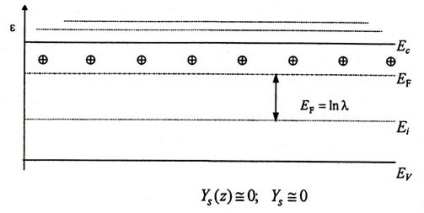
Рис .4.3. Енергетична діаграма області просторового заряду напівпровідника електронного типу провідності для деякого довільного значення поверхневого електростатичного потенціалу
З малюнка добре видно, що при наявності вигину зон значення енергії Фермі стає функцією коордінатиz. Звідси зрозуміло, що для будь-якої точки (або перетину паралельного поверхні) ОПЗ відповідно до законів статистики вираз для рівноважних концентрацій можна записати у вигляді
Із загальних міркувань і розгляду енергетичної діаграми на рис.4.3 видно, енергія Фермі в кожній точці визначається різницею вигину зон Ys і енергії Фермі в обсязі
Це дозволяє нам записати
Використовуючи формули (4.1.7), отримаємо
Зупинимося коротко на знаках введених EFs і Ys. Знак безрозмірного електростатичного потенціалу буде негативним при вигині зон вгору і позитивним при вигині вниз. EFs. а також і Ys .будут мати негативний знак, якщо рівень Фермі знаходиться на енергетичній діаграмі и нижній половині забороненої зони, і навпаки.
Співвідношення (4.2.7) фактично відображають використання для визначення поверхневих концентрацій ns і ps статистика Максвела-Больцмана. Раніше вже зазначалося, що дуже близько до дозволеної зоні. Фактор близькості визначається співвідношенням між одиницею експонентою в знаменнику формули (4.1.1). Якщо показати показник експоненти більше 3, то експонента на порядок перевищує едініцу- перехід до статистики Больцмана. В іншому випадку має місце виродження і необхідно користуватися статистикою Фермі.
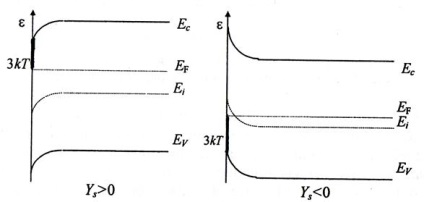
Мал. 4.4 .Енергетіческіе діаграми, що ілюструють граничні вигини зон
Для поверхні це означає, що будуть розглядатися такі вигини зон, при яких рівень Фермі на поверхні не наближається до країв дозволених зон ближче ніж на 2-3 k0 T.
Граничні вигини представлені на графіках рис.4.4
Розглянемо різні види ОПЗ, що виникають на кордонах розділу, спочатку якісно, ще до рішення рівняння Пуассона. Як приклад виберемо формування поверхневої ОПЗ для напівпровідника з досить сильно вираженим n-типом провідності. Це означає, що для нього виконується нерівність EF = ln # 955;> 3.
1. Плоскі зони. Ця ситуація зображується на енергетичній діаграмі з прямими зонами аж до поверхні (рис.4.5). Положення рівня Фермі на поверхні співпадає з таким в обсязі. Область просторового заряду не утворюється: # 961; (z) = 0
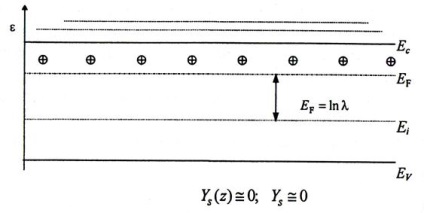
Рис.4.5. Енергетична діаграма для випадку плоских зон (область просторового заряду відсутній)
2. Збагачення. Необхідно відзначити, що цей і всі наступні терміни відносяться до зміни концентрації основних носіїв заряду. Наприклад, в даному випадку ясно, що збагачення означає збільшення концентрації основних носіїв в поверхневої ОПЗ. Ця область «збагатилася» основними носіями заряду-n (z)> n0. Для обраного в якості прикладу електронного напівпровідника це означає, що рівень Фермі на поверхні і в усій області просторового заряду розташовується ближче до зони провідності, ніж в обсязі. Все це відповідає вигину зон вниз. У вибраній систем е відліку цьому відповідає позитивне значення поверхневого електростатичного потенціалу-Ys> 0 (рис.4.6).
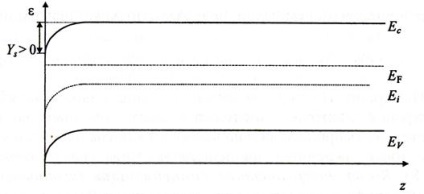
Рис.4.6. Енергетична діаграма поверхні напівпровідника n-типу, відповідна нагоди збагачення ns> n0
Якщо поверхнева концентрація ns не дуже велика в порівнянні з n0. то це слабке збагачення. Йому відповідають вигини зон Ys
При Ys> 3 настає сильне збагачення, коли ns >> n0. Зрозуміло, що при збагаченні концентрація дірок в області просторового заряду менше, ніж в обсязі, так як при рівновазі завжди np = ni 2.
3. Збідніння. Відповідно до прийнятого вище визначенням це стан має означати, що концентрація електронів в ОПЗ менше, ніж в обсязі n (z)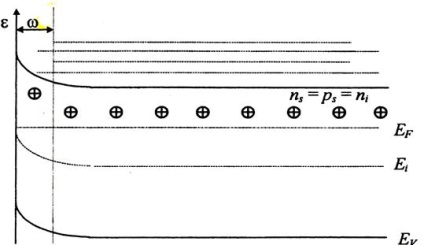
Рис.4.7. Енергетична діаграма поверхні напівпровідника n-типу, відповідна збіднення
При подальшому збільшенні вигину зон настає момент, коли концентраціями і електронів, дірок можна знехтувати в порівнянні з концентрацією іонізованих донорів. Отже, ці нерухомі донори і формують основну частину поверхневого заряду. Рівень Фермі на поверхні збігається з серединою забороненої зони на поверхні Ys = ln # 955 ;. Електрони як би відсуваються в обсяг на певну глибину W. обмежує явно виражений шар збіднення (рис.4.7).
Співвідношення об'ємних і поверхневих концентрацій при цьому
4. Інверсія. У міру збільшення негативного вигину зон концентрація електронів продовжує падати, а концентрація дірок зростає. Цей процес сильно прискорюється після переходу рівня Фермі нижче середини забороненої зони на поверхні (рис.4.8)