Теорія систем автоматичного управління
Якщо на автоматичну систему діють одночасно корисний сигнал і перешкода, то виникає задача оптимального розрахунку системи з тим, щоб отримати найменшу результуючу помилку. З точки зору найкращого відтворення корисного сигналу система повинна мати якомога більшу смугу пропускання, а з точки зору найкращого придушення перешкоди система, навпаки, повинна мати можливо меншу смугу пропускання. Критерієм отримання оптимального рішення тут буде мінімальне значення результуючої помилки системи, яка визначається корисним сигналом і перешкодою.
Для випадкових величин найбільш просто визначити середньоквадратичнепомилку, тому її і використовують для опеньки точності автоматичної системи.
Розглянемо розрахунок системи за критерієм мінімуму середньоквадратичної помилки при одночасній дії корисного сигналу і перешкоди.
Згідно з цим критерієм небажаність помилки пропорційна квадрату її величини. Така постановка є часто логічною, але вона не може, звичайно, претендувати па повну універсальність. У деяких випадках, наприклад при стрільбі по будь-якої мети, всі помилки, великі деякого значення, є однаково небажаними. Однак середній квадрат помилки системи управління
в переважній більшості випадків є найбільш просто обчислюється величиною, що і визначило використання цього критерію.
Можливі кілька формулювань завдання. Найбільш просто задача може бути сформульована так. Якщо є якась система автоматичного управління заданої структури, то необхідно так вибрати параметри цієї системи, щоб отримати мінімум середньоквадратичної помилки при заданих статистичних характеристиках корисного сигналу і перешкоди.
Це завдання вирішується таким чином. За спектральної щільності помилки шляхом її інтегрування знаходиться дисперсія. Дисперсія виходить залежить від імовірнісних характеристик корисного сигналу, перешкоди і параметрів системи. Потім шукаються умови, які повинні бути накладені па параметри системи, щоб отримати мінімум дисперсії. При досить простому вираженні для дисперсії це може бути визначено безпосереднім диференціюванням і прирівнянням нулю приватних похідних.
У більш складних випадках доводиться шукати мінімум дисперсії шляхом числового завдання цікавлять параметрів і побудови відповідних графіків, а також розрахунком на ЕОМ.
деякою формулою перетворення
- завдання диференціювання, при Н
- статистичне упередження (прогноз) і т. А.
викладеного помилку системи можна представити у вигляді
- вагова функція замкнутої системи.
Підставляючи (11.130) і (11.131) у формулу (11.129), одержуємо
Завдання полягає в тому, щоб знайти частотну передавальну функцію замкненої системи, пов'язану з ваговою функцією перетворенням Фур'є
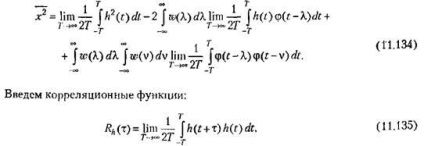
Розкриємо в вираженні (11.132) дужки і змінимо порядок інтегрування:
В результаті вираз (11.134) можна перетворити до вигляду
то нижні межі інтегрування в (11.138) треба покласти рівними нулю. В результаті отримаємо
З останнього виразу видно, що оптимальна вагова функція, відповідна мінімуму середнього квадрата помилки, визначається тільки видом кореляційних функцій корисного сигналу і перешкоди.
Можна показати [88], що необхідна і достатня умова мінімізації виразу (11.139), яке повинно бути накладено на вагову функцію, полягає в тому, щоб вона була рішенням інтегрального рівняння Вііера-Хопфа
Оптимальна передавальна функція (11.133), відповідна оптимальної вагової функції, що є рішенням рівняння (11.140), може бути представлена у вигляді
т. е. в так званому випадку оптимального згладжування, маємо
У цьому випадку рішення (11.1-11) може бути представлено в більш простому вигляді:
Чисельник цього виразу визначається наступним чином. Розглянемо такий вираз:
-
При реалізації в системі оптимальної передавальної функції вийде теоретичний мінімум середнього квадрата помилки. Цей мінімум визначається виразом
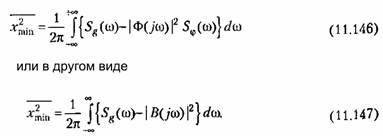
Розглянемо ілюстративний приклад. Припустимо, що корисного сигналу і
заваді на вході системи відповідають спектральні щільності:
Іайдйм спектральну щільність, відповідну (11.136):

Відкинувши перший член в дужках, відповідний полюсу в нижній півплощині, знаходимо чисельник шуканої передавальної функції (11.143):

Знаходження оптимальної передавальної функції ще не означає, що реальна автоматична система може бути виконана оптимальної, так як реалізація її може бути пов'язана з великими труднощами. Оптимальну передавальну функцію, за винятком найпростіших випадків, слід вважати ідеальною функцією, до якої але можливості треба прагнути при виконанні реальної автоматичної системи. Теорія оптимальних систем викладається в роботах [22, 88, 89].