• За характером обліку просторової роботи - одно-, дво- і тривимірні.
• По виду невідомих - дискретні, дискретно-континуальні і контінуальниє.
• По виду конструкцій, покладених в основу розрахункової схеми - стрижневі, пластинчасті, оболонкові і масивні.
• По обліку інерційних сил - статичні і динамічні.
Елементи розрахункової схеми
Розрахункова схема складається з умовних елементів: стрижнів. пластин. оболонок, масивів і зв'язків.
Стрижні використовують в розрахункових схемах стрижневих конструкцій (стійок, балок. Арок і ін.), Систем з таких конструкцій (ферм. Рам. Сітчастих оболонок), а також для наближеного розрахунку площинних конструкцій (наприклад, несучих стін будівель).
Пластини трикутної і прямокутної форми є основними кінцевими елементами при розрахунку методом кінцевих елементів площинних конструкцій (стін і плит перекриттів будівель).
Оболонки є розрахунковою схемою різних просторових конструкцій (куполів, склепінь, оболонок).
Масиви в розрахункових схемах використовуються, як правило, в якості недеформівних опор прогонових конструкцій, що спираються на стискати підставу.
Зв'язки в розрахункових схемах з'єднують між собою окремі елементи, а також конструкцію з підставою. У розрахункових схемах зв'язку розрізняються за кількістю ступенів свободи, які вони забирають від системи. Зв'язки можуть бути дискретні і розподілені (контінуальниє). Стрижні і пластини, з'єднані розподіленими зв'язками називаються складовими стрижнями і пластинами. [1]
Розрахункові схеми багатоповерхових будівель
Багатоповерховий будинок є складною просторовою системою, яка в залежності від поверховості, особливостей конструктивної системи і діючих навантажень, розраховується з різним ступенем деталізації з використанням різних розрахункових схем. У сучасній практиці проектування розрахунок будівлі, як правило, виконується за спеціальними програмами із застосуванням обчислювальної техніки. [2] [3]
При одновимірної розрахунковій схемі будівля розглядається як консольний тонкостінний стержень або система стрижнів, пружно або жорстко закріплених в підставі. Передбачається, що поперечний контур стрижня або системи стрижнів незмінним.
При двомірної розрахунковій схемі будівля розглядається як плоска конструкція, здатна сприймати тільки таку зовнішню навантаження, яка діє в її площині. Для визначення зусиль у вертикальних несучих конструкціях умовно приймається, що всі вони розташовані в одній площині і мають однакові горизонтальні переміщення в рівні перекриттів.
При тривимірної розрахункової схемою будівля розглядається як просторова система, здатна сприймати прикладену до неї просторову систему навантажень.
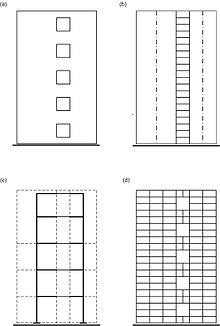
Двомірні розрахункові схеми стіни з регулярно розташованими по вертикалі прорізами (a): складеного стержня (b); багатоповерхова рама (c); пластинчатая система МСЕ (d)
У дискретних розрахункових схемах невідомі зусилля або переміщення визначають для кінцевого кількості вузлів системи шляхом вирішення систем алгебраїчних рівнянь. Дискретні розрахункові схеми найбільш пристосовані для розрахунку методом кінцевих елементів. Такі схеми широко використовують для моделювання не тільки стрижневих систем, але і суцільних пластин і оболонок.
У континуальних розрахункових схемах невідомі силові фактори або переміщення задають у вигляді безперервних функцій уздовж двох або трьох координатних осей. Невідомі функції визначаються рішенням крайової завдання для системи рівнянь в приватних похідних. В окремих випадках застосування континуальної розрахункової схеми дозволяє отримати рішення у вигляді кінцевих формул. Однак ці випадки досить рідкісні. Тому така розрахункова схема застосовується рідко.
Приклади двомірних розрахункових схем стіни з прорізами, є вертикальною діафрагмою жорсткості будівлі, показані н малюнку праворуч.
- ↑ Ржаніцин А. Р. Складові стрижні і пластини. М. Стройиздат, 1986.
- ↑ 12Лішак В. І. Розрахунок безкаркасних будівель із застосуванням ЕОМ. М. Стройиздат, 1977.
- ↑ Посібник з проектування житлових будинків. Вип. 3. Конструкції житлових будинків (до СНиП 2.08.01-85). М. Стройиздат, 1989.
- ↑ Ржаніцин А. Р. Робота зв'язків в складових стрижнях. Наук. тр. МІСД ім. В.В. Куйбишева, 1938, № 2: с. 29-32.
- ↑ Ржаніцин А. Р. Теорія складових стрижнів будівельних конструкцій. М. Стройиздат, 1948: 192 с.
- ↑ Ржаніцин А. Р. Мілейковський І. Е. Розрахунок оболонки каркаса висотній частині палацу культури та науки у Варшаві на вітрове навантаження. - Будівельна промисловість, 1954, № 2, с. 24-28.
- ↑ Rosman R. Approximate analysis of sher walls subtect to literal loads / ACI J. Procttdings, 1964, 61 (6): pp. 717-733.
- ↑ Дроздов П. Ф. Розрахунок великопанельних будинків на вертикальні і горізонтальнин навантаження. - Будівельна механіка і розрахунок споруд, 1966, № 6, с. 1-6.
- ↑ Подільський Д. М. Розрахунок об'ємних елементів жорсткості будівель підвищеної поверховості. - Будівельна механіка і розрахунок споруд, 1968, № 1: с. 57-62.
- ↑ Власов В. З. Тонкостінні просторові системи. М. Госстройіздат, 1958.
- ↑ Лишак В. І. До розрахунку великопанельних будинків підвищеної поверховості - Будівельна механіка і розрахунок споруд, 1969, № 1: с. 16-21.
- ↑ Вольфсон Б. П. Розрахунок будівель як збірних (монолітних) тонкостінних просторових систем. - Будівельна механіка і розрахунок споруд, 1972, № 5.
- Ржаніцин А. Р. Будівельна механіка. М. «Вища школа», 1982.