Розрахунок циліндричного евольвентного зубчастого зачеплення (зовнішнього і внутрішнього), оптимальний розрахунок коефіцієнтів зміщення для прямозубого зовнішнього зачеплення і розрахунок профілю зуба.
1. Не повинно бути підрізання ніжки зуба;
2. Не повинно бути інтерференції зубів;
3. Не повинно бути загострення зубів, тобто товщина зуба на поверхні вершин не повинна бути - Sa1, Sa2 <0.3m;
4. Коефіцієнт перекриття - Ea> 1.0. в літературі рекомендується, щоб коефіцієнт перекриття був> 1.2.
5. Коефіцієнти питомої ковзання повинні бути близькі один до одного, а в кращому випадку рівні, тоді знос зубів буде відносно рівномірним.
Все це закладено в побудові блокуючих контурів: см. ГОСТ- 16532-70 і ГОСТ - 19274-73, але, на жаль, там наведені не всі можливі випадки поєднання кількості зубів шестерень і коліс.
Комп'ютера доводиться виробляти колосальну кількість обчислень при розрахунку коефіцієнтів зміщення X1 і X2.
Наприклад: при обчисленні тільки одного кута зачеплення, для досягнення необхідної точності, потрібно 5000 циклів, і всі ці обчислення відбувається до тих пір, поки всі наведені вище параметри не вкладуться в заданий проміжок, що задовольняє всім вимогам до даного зубчатому зачеплення. На малюнку нижче, показаний «оптимальний» розрахунок зовнішнього евольвентного зубчастого зачеплення зі зміщенням. Як бачите, все вище перераховані вимоги до зачеплення, виконуються.
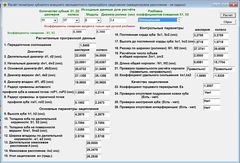
А, ось той же самий розрахунок, виконаний програмою, згідно з ГОСТ-16532-70.
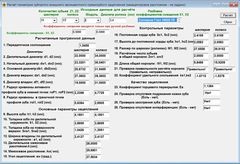
Коефіцієнт торцевого перекриття, в даному випадку, вже не досягає оптимального Ea = 1.2.
Розроблена програма дозволяє розрахувати всі дані для побудови профілю зуба. Формули для розрахунку взяті з ГОСТ - 16532-70. Це дозволило провести побудова профілю зубів з високим ступенем точності. Нижче на малюнку показано побудову зуба шестерні, евольвентного зачеплення, коли: Z1 = 11, Z2 = 25, m = 5, x1 = 0.5, x2 = 0.5.
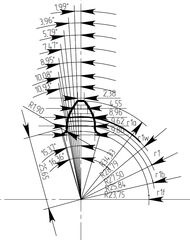
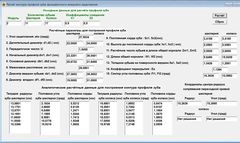
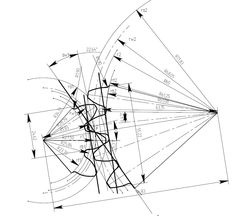
Точність побудови креслення підтверджується зняттям розмірів безпосередньо з креслення: кількість зубів в загальній нормалі шестерні і колеса, а також довжина загальної нормалі, відповідають розрахунковим.